1.1 O básicos sobre erros#
De modo geral, a resolução de um problema, em ciências e engenharia, passa necessariamente por três etapas distintas:
A observação e entendimento do(s) fenômeno(s) envolvido(s);
A construção de um modelo matemático que represente o problema;
A resolução do modelo matemático por métodos numéricos ou analíticos.
As duas primeiras etapas consistem na fase de modelagem e a terceira é a fase de resolução. Tanto na fase de modelagem quanto na fase de resolução podem ocorrer erros, mesmo que esses erros não tornem a resposta obtida inválida ou inútil. Em geral busca-se uma solução aproximada, dentro de uma precisão pré-estabelecida.
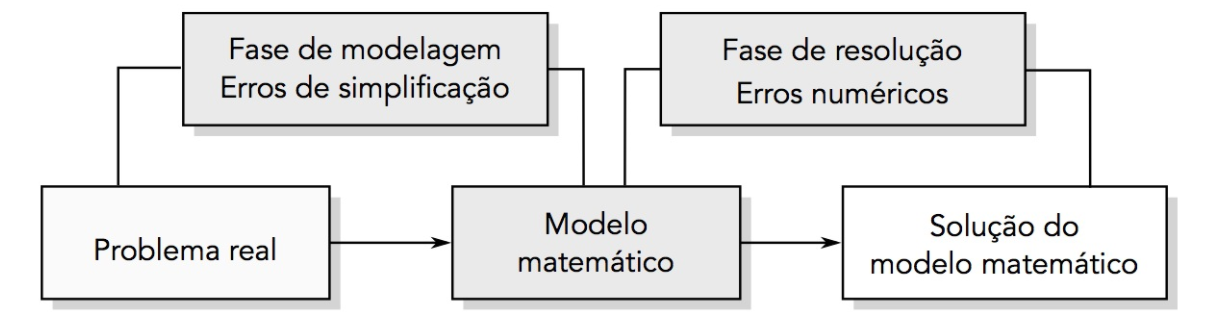
Fonte: Arenalles e Darezzo, 2016.
Os erros na fase de modelagem podem ser decorrentes de medições imprecisas, erros de anotação, simplificações e deduções equivocadas. Os erros na fase de resolução ocorrem devido a erros de cálculo, escolha de um método ineficaz, aproximações numéricas ou arredondamentos. Dizemos que métodos analíticos de resolução geram soluções exatas e métodos numéricos geram soluções aproximadas.
A maioria dos problemas envolvendo fenômenos reais produzem modelos matemáticos cuja solução analítica é difícil (ou impossível) de se obter, mesmo quando provamos que a solução existe. Nesses casos usamos métodos numéricos, os quais fornecem soluções aproximadas, que apesar de, em geral, serem diferentes da solução exata, podem ser suficientemete próximas para que sejam úteis em suas aplicações.
Representação de números em ponto flutuante#
Os métodos numéricos são especialmente úteis quando utilizamos computadores para realizar os cálculos, no entanto, existem limitações na capacidade de armazenar certos números internamente. A representação de números reais nas máquinas é feita, geralmente, utilizando o sistema de ponto flutuante normalizado e base binária. Ou seja, os números reais são armazenados em um conjunto fixo de bits. Cada bit pode assumir somente dois valores, 0 ou 1 (corte ou passagem de energia, respectivamente), dessa forma, nem todos os números reais podem ser representados de forma exata. Vamos entender isso um pouco melhor com os argumentos a seguir.
Sabemos que o número \(0.125\), na base decimal, pode ser escrito como
ou, equivalentemente,
De forma análoga, a fração binária de valor idêntico \(0.001\) pode ser escrita como
Nesse caso os denominadores das parcelas são potências de \(2\), ou seja, podemos escrever
No sistema de ponto flutuante normalizado (SPFN), um número é representado apenas pela sua forma fracionária, em que apenas um número finito de algarismos são armazenados (algarismos significativos), além do expoente da base e o sinal.
Por exemplo, o número \(1.2345\) na base decimal será representado como
em que \(12345\) são os algarismos significativos e 1 é o expoente da base 10.
A maioria das máquinas que usamos atualmente operam na base 2 (binária) em que os algarismos disponíveis são 0 e 1. O número decimal \(1.2\), pode ser representado na base binária pelo número \(1.00110011001100110011 \overline{0011}\) que tem infinitas casas após a vírgula, portanto nem todos algarismos significativos poderão ser armazenados. Supondo que apenas 10 algarismos possam ser armazenados, sua respresentação será
No SPFN apenas os dígitos \(1001100110\), o sinal (0 para positivo e 1 para negativo) e o expoente \(1\) precisam ser armazenados para representar o número.
Exemplo 1.1.1: Para converter um inteiro decimal em binário, podemos usar a função bin() do Python. O resultado será uma stringo com o prefixo '0b' no começo. Veja alguns exemplos:
bin(22)
'0b10110'
Observe o que acontece fazendo a operação \(1\times2^4+0\times2^3+1\times2^2+1\times2^1+1\times2^0\), como é mostrado a seguir
1*2**4 + 0*2**3 + 1*2**2 + 1*2**1 + 0*2**0
22
Use esse exemplo para testar outros números inteiros.
Padrão IEEE#
Em geral, uma máquina com 32 bit utiliza 23 bit para armazenar os algarismos da parte fracionária, 8 bit para os algarismos do expoente da base e 1 bit para armazenar o sinal. Para 64 bits, são 52 bits de digitos significativos, 11 bits para o expoente e 1 bit para o sinal.
O esquema para 32 bits é ilustrado na figura abaixo.
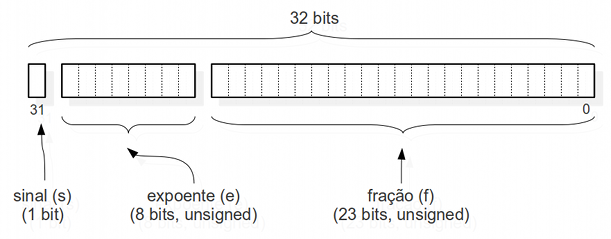
O padrão IEEE 754 é atualmente o mais utilizado para representar números reais. Na precisão float usa 23 bits, para a parte fracionária, 8 bits para o expoente e 1 bit para o sinal. Na precisão double, usa 52 bits, para a parte fracionária, 11 bits para o expoente e 1 bit para o sinal, o que permite representar valores entre \(2^{-1022}\) até \(2^{1023}\). Alguns exemplos de representações do numero zero, infinito e “não número”.

Alguns exemplos de tipos de dados disponíveis no módulo numérico Numpy (numpy.org) são mostrados abaixo para o caso de um

Alguns números, como os irracionais ou a fração 1/3, por exemplo, têm representações fracionárias com infinitas casas decimais. Então, para serem computados precisam ser truncados ou arredondados. Além disso, alguns números com representação decimal finita, possuem representação binária infinita, e vice versa. Assim, erros de arredondamento podem ocorrer no processo de conversão entre bases e, também, nas operações aritméticas de ponto flutuante.
Exemplo 1.1.2: Observe o que acontece se fazemos \(x=\frac{1}{3}\) e, então espera-se obter \(x\times 10 \times 0.3 = \frac{1}{3} \times 3 = 1\). vejamos o que acontece computacionalmente.
x = 1/3
x
0.3333333333333333
x*10*0.3
0.9999999999999999
Tente fazer \(x\times (10 \times 0.3)\) e tente explicar o que você observou nos resultados obtidos.
Conversão entre bases#
Usualmente, utilizamos o sistema de numeração decimal para representar números. Esse é um sistema de numeração posicional onde a posição do dígito indica a potência de 10 que o dígito representa. Por exemplo, o número 293 é decomposto como 293 = 2 centenas +9 dezenas + 3 unidades. O sistema de numeração posicional também pode ser usado com outras bases.
Dado um número real, \(N\), é sempre possível representá-lo em qualquer base \(b\), da seguinte forma
em que \(a_i \in \{0,1,2,3,...,(b-1)\}\), com \(n\) e \(m\) inteiros.
Base binária#
Exemplos 1.1.3: (Fonte: Arenalles e Darezzo, 2016)
a) \((1011)_2 = 1 \times 2^0 + 1 \times 2^1 + 0 \times 2^2 + 1 \times 2^3\)
b) \((111.01)_2 = 1 \times 2^{-2} + 0 \times 2^{-1} + 1 \times 2^0 + 1 \times 2^1 + 1 \times 2^2 \)
Base decimal#
Exemplos 1.1.4: (Fonte: Arenalles e Darezzo, 2016)
a) \((231)_{10} = 1 \times 10^0 + 3 \times 10^1 + 2 \times 10^2\)
b) \((231.35)_{10} = 5 \times 10^{-2} +3\times 10^{-1} +1 \times 10^0 + 3 \times 10^1 + 2 \times 10^2\)
c) Podemos facilmente converter um número binário para a base decimal escrevendo o número em formato de somatória e realizando as ‘contas’ no sistema decimal, com é mostrado a seguir
\((1001.101)_2 = \)
\( 1\times 2^{-3} + 0\times 2^{-2} + 2\times 10^{-1} +1 \times 2^0 + 0 \times 2^1 + 0 \times 2^2 + 1 \times 2^3 = \)
\( 1/8 + 0/4 + 1/2 + 1/1 + 0 \cdot 2 + 0 \cdot 4 + 1 \cdot 8 =\)
\(0.125+0.5+1.0+8.0 =\)
\(9.625\)
Assim \((1001.101)_2 = (9,625)_{10}\).
A mudança de base decimal para binária, no caso de um número inteiro, é realizada dividindo o número sucessivamente por 2 até obter o quociente 1. Então, toma-se o quociente e os restos das divisões na ordem contrária em que foram obtidos para formar o número binário. Vejamos um exemplo.
Exemplo 1.1.5: (Fonte: Arenalles e Darezzo, 2016)
O número 25, na base 10, pode ser convertido para a base 2 procedenco sucessivas divisões por 2 como é mostrado abaixo.
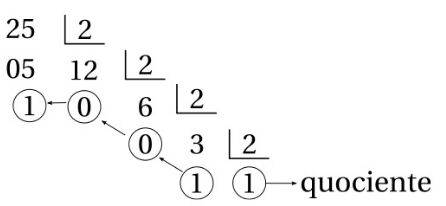
Tomando-se o quociente 1 e os restos das divisões na ordem contrária em que foram obtidos, formamos o número binário 11001. Assim,
Exercício 1.1.6: Faça um programa em Python para converter um inteiro decimal em um binário. Teste para o número \((11)_{10}=(1011)_2\). Dica: o operador % usado no lugar do operador / em uma divisão, retorna o resto dessa divisão.
11%2
1
Para converter uma fração decimal para a base binária procedemos sucessivas multiplicações por 2. A parte inteira do resultado obtido será o primeiro dígito binário. A parte fracionária será multiplicada novamente por 2 para obter-se os próximos dígitos no número binário, sucessivamente. vejamos um exemplo.
Exemplo 1.1.7:
O número \((0.1875)_{10}\) pode ser convertido para a base binária procedendo como é mostrado na figura abaixo

Assim, obtemos que \((0.1875)_{10}=(0.0011)_2\).
Exercício 1.1.8: Converta os números \((13.25)_{10}\) e \((0.2)_{10}\) para a base binária.
Exercício 1.1.9: Faça um programa em Python para converter um número qualquer da base decimal para a base binária. Dica: para pegar a parte inteira podemos usar a função floor da biblioteca math do Python.
# por exemplo
from math import floor
floor(13.25)
13
Outras bases#
Exemplo 1.1.10: Em Python existem funções para representar números em diferentes bases, incluindo os sistemas octogonal e hexadecimal. Para converter um inteiro em um binário, octal, ou hexadecimal, podemos proceder como é mostrado abaixo
x = 1234
print ('Binário: x =', bin(x))
print ('Octal: x =', oct(x))
print ('Hexadecimal: x =', hex(x))
Binário: x = 0b10011010010
Octal: x = 0o2322
Hexadecimal: x = 0x4d2
Ou, alternativamente
print ('Binário: x =', format(x, 'b'))
print ('Octal: x =', format(x, 'o'))
print ('Hexadecimal: x =', format(x, 'x'))
Binário: x = 10011010010
Octal: x = 2322
Hexadecimal: x = 4d2
Exercícios:
(Fontes: Ruggiero (2016), Chapra e Canale (2016))
1. Converta os seguintes números decimais para sua forma binária:
a) \((37)_{10}\)
b) \((2345)_{10}\)
c) \((0,1217)_{10}\)
d) \((71,263)_{10}\)
e) \((3,147)_{10}\)
f) \((625,125)_{10}\)
2. Converta os seguintes números na base 2 para a base 10:
a) \((101101)_{2}\)
b) \((101,101)_{2}\)
c) \((110101011)_{2}\)
d) \((0,1101)_{2}\)
e) \((0,111111101)_{2}\)
f) \((0,01101)_{2}\)
Respostas:
1. \(a) (100101)_{2} \quad b) (100100101001)_{2} \quad c) (0,000111110010)_{2}\) \(d) (1000111,010000110101...)_{2} \quad e) (11,0010010110100...)_{2} \quad f) (1001110001,001)_{2}\)
2. \(a) (45)_{10} \quad b) (5,625)_{10} \quad c) (427)_{10} \quad d) (0,8125)_{10} \quad e) (0,994140625)_{10} \quad f) (0,40625)_{10} \quad\)
