2.1 Localização de raízes

2.1 Localização de raízes#

Em ciências e engenharias frequentemente a solução de um problema real é obtida resolvendo uma equação em uma variável real, a qual sempre pode ser escrita na forma $$f(x)=0$$

Dada uma função $f:R \rightarrow R$ dizemos que $\overline{x} \in R$, tal que $f(\overline{x})=0$ é um zero (ou raiz) da função $f$. Graficamente, uma raíz é o ponto onde a função $f(x)$ cruza ou toca o eixo $x$. Uma equação $f(x)=0$ pode não ter solução (raiz) real, ter uma única raiz ou várias.

Quando a equação é simples, o valor de $x$ pode ser determinado analiticamente. Esse é o caso quando se escreve $x$ explicitamente após a aplicação de operações matemáticas, ou quando uma fórmula conhecida (como a fórmula de Bháskara para resolução de equações quadráticas) pode ser usada para determinar o valor exato de $x$. Em muitas situações, no entanto, é impossível determinar analiticamente a raiz de uma equação.

Por exemplo, é relativamente fácil obter analiticamente as raízes das equações

a) $2.1x-47.3 = 0$

b) $x^2+2x-3 = 0$

c) $senx-x = 0$

Já para as equações a seguir é preferível utilizar-se de métodos numéricos

a) $xe^x-2 = 0$

b) $cos3\theta-sen\theta =0$

c) $2.1^x+5.7x=0$

Exemplo 2.1.1: Em termodinâmica, sob determinadas condições, a relação entre o calor $Q$ fornecido a um gás e sua variação de temperatura $T_f - T_i$ é dada por

\[ Q = nR \left[ A (T_f-T_i)+ \frac{B}{2}(T_f^2-T_i^2) + \frac{C}{3}(T_f^3-T_i^3) \right].\]

Para o gás metano tem-se $R=8,314 J/mol.K$, $A=1,702$, $B=9,081 \times 10^{-3}K^{-1}$, $C=-2,164 \times 10^{-6} K^{-2}$.

Considere o problema de calcular a temperatura final $T_f$ se $20 kJ$ de energia que é absorvido pelo gás, supondo estar contido em uma uma câmara com $n=2 mol$ de metano a temperatura $T_i = 300 K$.

Exemplo 2.1.2: A área do segmento $A_S$ de um círculo de raio $r$ (ver figura abaixo) é dada por $A_S=\frac{1}{2}r^2(\theta-sen\theta).$

Para se determinar o ângulo $\theta$ se $A_S$ e $r$ são conhecidos, a equação deve ser resolvida para $\theta$. Não é uma tarefa simples escrever $\theta$ explicitamente em termos de $A_S$ e $r$, portanto, pode não ser possível resolver essa equação analiticamente.

Exemplo 2.1.3: Seja uma esfera de madeira de raio $r$ colocada a flutuar sobre a água conforme figura. Qual é a altura $d$ da esfera que ficará submersa?

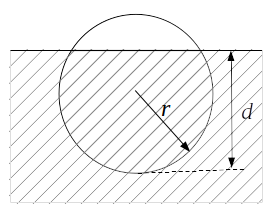
Para responder essa pergunta, observemos que, pelo Princípio de Arquimedes o peso da esfera deve ser equilibrado com o peso do volume de água deslocada, ou seja, $\mu_e V_e g = \mu_a V_a g$ onde $g$ é a aceleração da gravidade, $\mu_e$ é a densidade relativa da madeira e $\mu_a$ é a densidade relativa da água, $V_e$ e $V_a$ são os volumes. Essa equação nos leva a

\[ \mu_e \frac{4 \pi r^3}{3} = \mu_a \int_0^d \pi \left[r^2-(x-r)^2) \right]dx \]

\[ \mu_e \frac{4 \pi r^3}{3} = \mu_a \frac{\pi d^2 (3r-d)}{3}\]

substituindo os valores $r=10 cm$, $\mu_e =0,638 g/cm^3$ e $\mu_a=1 g/cm^3$, com $\pi \approx 3.1415$, podemos chegar à seguinte equação aproximada

\[ 1.047d^3-31.415d^2+2672.369=0\]

Basta resolver essa equação para obter a resposta procurada.

No entanto, encontrar a solução analítica para esse problema não é tão simples, mas com uma rotina numérica simples podemos encontrar uma boa aproximação.

Observe que poderíamos ter multiplicado ambos os lados da equação por $\frac{3}{\pi}$, o que nos daria

\[d^3-30d^2+2552=0\]

que é uma equação mais precisa, uma vez que não tivemos que usar aproximações, no entanto esse tipo de simplificaçao requer manipular o número $\pi$ como um símbolo. Veremos que frequentemente soluções numéricas geral soluções aproximadas

Exemplo 2.1.4: Podemos utilizar uma abordagem numérica para obter soluções aproximadas de equações, vejamos por exemplo a equação $f(d) = 1.047d^3-31.415d^2+2672.369$ do exemplo descrito anteriormente. Dos dados do problema, podemos inferir que a solução é um número entre 0 e 20, então, calculamos valores da função nesse intervalo e tentar encontrar uma aproximação. Buscamos o valor de $d$ que anula a função $f$, então, observando os resultados na tabera abaixo, podemos concluir que a solução é um número entre 11 e 12 cm pois é o intervalo onde a função muda de sinal.

for d in range(0,21):
    y = 1.047*d**3-31.415*d**2+2672.369
    print('f(',d,')=', round(y,3))

f( 0 )= 2672.369
f( 1 )= 2642.001
f( 2 )= 2555.085
f( 3 )= 2417.903
f( 4 )= 2236.737
f( 5 )= 2017.869
f( 6 )= 1767.581
f( 7 )= 1492.155
f( 8 )= 1197.873
f( 9 )= 891.017
f( 10 )= 577.869
f( 11 )= 264.711
f( 12 )= -42.175
f( 13 )= -336.507
f( 14 )= -612.003
f( 15 )= -862.381
f( 16 )= -1081.359
f( 17 )= -1262.655
f( 18 )= -1399.987
f( 19 )= -1487.073
f( 20 )= -1517.631

Seguindo o mesmo procedimento mas agora incrementando o valor de $d$ em 0.1 e calculando $f$ para valores de $d$ entre 11 e 12 observamos que a solução está entre $11.8$ e $11.9$.

for inc in range(0,11):
    d = 11+inc/10
    y = 1.047*d**3-31.415*d**2+2672.369
    print('f(',d,')=', round(y,3))

f( 11.0 )= 264.711
f( 11.1 )= 233.637
f( 11.2 )= 202.631
f( 11.3 )= 171.701
f( 11.4 )= 140.852
f( 11.5 )= 110.091
f( 11.6 )= 79.425
f( 11.7 )= 48.858
f( 11.8 )= 18.399
f( 11.9 )= -11.948
f( 12.0 )= -42.175

Por fim, podemos tomar como solução aproximada o ponto médio entre $11.8$ e $11.9$, ou seja, $d=11.85$. A precisão é de $0.05$.

Exemplo 2.1.5: (Usando a biblioteca SciPy)

Encontrando a raiz de $A_S=\frac{1}{2}r^2(\theta-sen\theta)$ com $r=1$ e $A_s = 3.5$.

from scipy.optimize import fsolve
import numpy as np

As = lambda x: 0.5*(x-np.sin(x))-3.5

sol = fsolve(As, 1)
print (sol)

[7.99067236]

Esses foram pequenos exemplos de como os métodos numéricos podem nos auxiliar a obter soluções aproximadas quando não é fácil ou possível obter soluções analíticas. Os métodos numéricos são utilizados para muitas outras situações, como resolver integrais definidas, sistemas lineares de grande porte, equações diferenciais, obter visualização de grandes conjuntos de dados, etc.

Nos casos em que uma solução exata $\overline{x}$ da equação $f(x)=0$ não puder ser encontrada por processos analíticos, uma solução aproximada pode ser obtida por métodos numéricos. Em geral, esses métodos fornecem uma sequência de aproximações, obtidas por um processo iterativo que termina quando a precisão desejada é atingida.

Encontrar numericamente a raiz de uma equação requer duas etapas:

Isolar a raiz, ou seja, encontrar um intervalo $[a,b]$ contendo uma única raíz da equação $f(x)=0$ e;
Refinar o intervalo que contém a raíz até atingir a precisão desejada.

Para isolar os zeros de uma função, podemos utilizar métodos gráficos ou testar valores numericamente.

Localização por métodos métodos gráficos#

Graficamente as raízes da equação $f(x)=0$ (ou zeros da função $f$ correspondem aos pontos onde o gráfico de $f$ intercepta o eixo $x$. Na figura abaixo, a função $f$ possui 5 zeros representados por $\overline{x}_1$, $\overline{x}_2$, $\overline{x}_3$, $\overline{x}_4$ e $\overline{x}_5$.

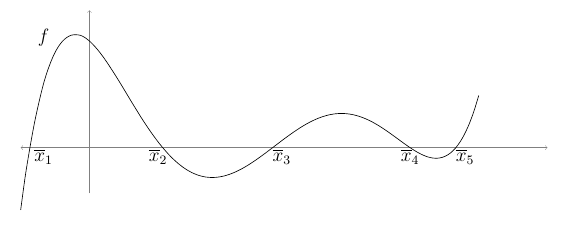
Nem sempre é fácil esboçar o gráfico de uma função sem a ajuda de um computador. Em muitos casos é conveniente rescrever a equação $f(x)=0$ numa forma equivamente $f_1(x)=f_2(x)$ e esboçar os gráficos de $f_1$ e $f_2$ para verificar onde eles se interceptam. Outra abordagem seria atribuir valores arbitrários para a variável $x$ e encontrar um par $a$ e $b$ tal que $f(a)\cdot f(b)<0$.

Exemplo 2.1.6:

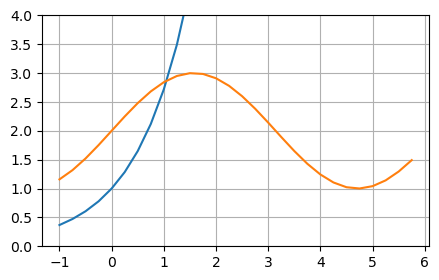
A equação $f(x)=e^x-sen(x)-2=0$ pode ser escrita como $e^x=senx+2$ então, esboçando os gráficos de $f_1(x)=e^x$ e $f_2(x)=senx+2$, observamos que a raiz procurada está entre $0.5$ e $1.5$, como pode ser visto no gráfico a seguir.

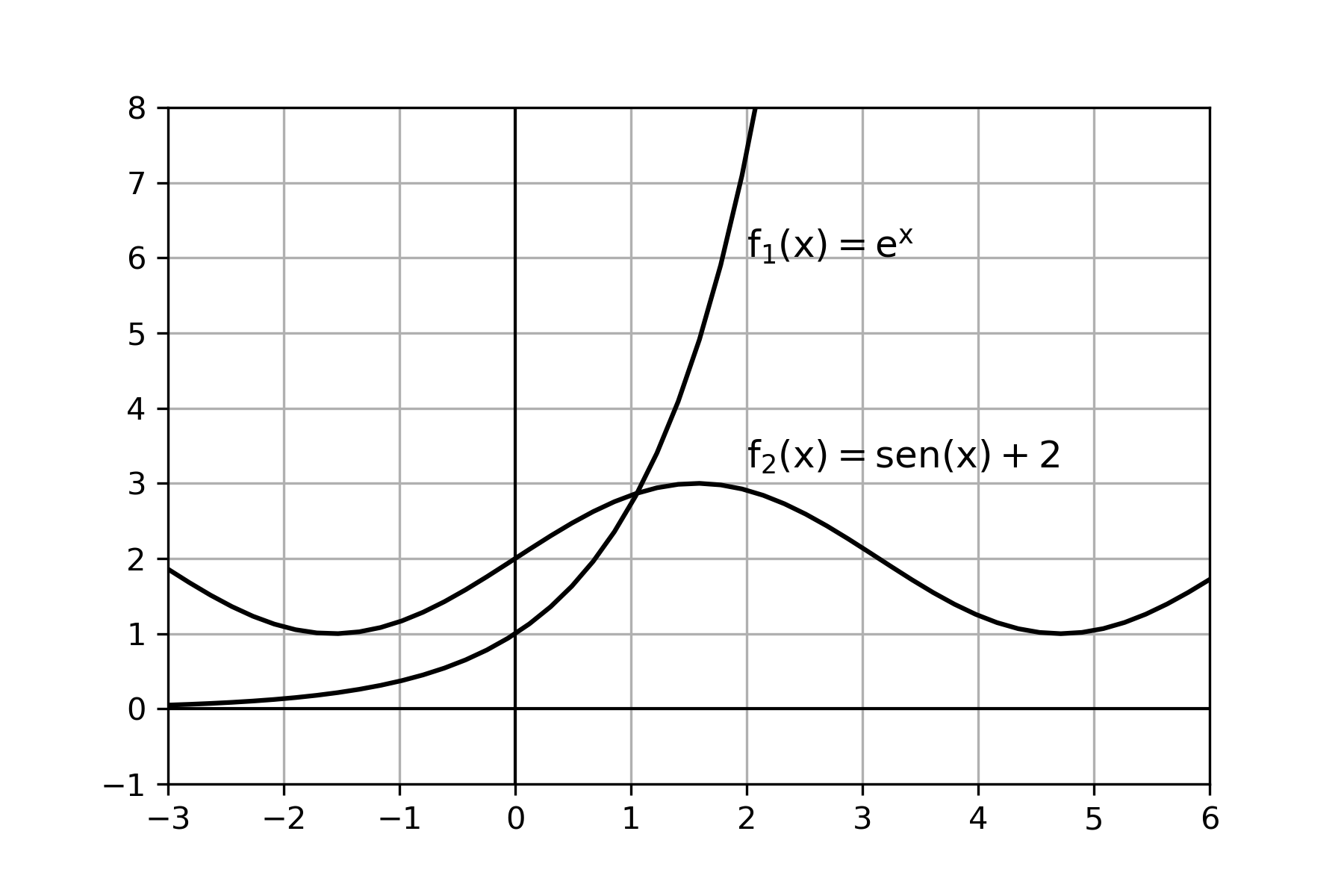
Vamos geraresses gráficos usando Python. Para isso precisamos da seguinte biblioteca:

import matplotlib.pyplot as plt

A partir daí criamos uma lista de pontos para plotar, fica fácil fazer isso usando a função arange da biblioteca numpy:

import numpy as np
x = np.arange(-1, 6, 0.25) # início, fim, passo
print (x)

[-1.   -0.75 -0.5  -0.25  0.    0.25  0.5   0.75  1.    1.25  1.5   1.75
  2.    2.25  2.5   2.75  3.    3.25  3.5   3.75  4.    4.25  4.5   4.75
  5.    5.25  5.5   5.75]

Agora definimos as funções para obter os valores de $f1(x)$ e $f2(x)$. Isso pode ser feito usando a função lambda ou def.

f1 = lambda x: np.exp(x)
f2 = lambda x: np.sin(x)+2

Agora, basta plotar:

plt.figure(figsize=(5,3))
plt.plot(x, f1(x), x, f2(x))
plt.ylim(0, 4) 
plt.grid()
plt.show()

../_images/2daef026453c0fdb81f67477b0e3f188309357affc16974d02ca958aaa045192.png

Exemplo 2.1.7: Atribuindo valores para $x$ e avaliando a função $f(x)=e^x-sen(x)-2$ para esses valores obtemos:

f(0.0) = -1.0000  
f(0.5) = -0.8307  
f(1.0) = -0.1232  
f(1.5) = 1.4842 
f(2.0) = 4.4798 
f(2.5) = 9.5840 

Como $f(1.0) \cdot f(1.5)<0$, podemos concluir que existe pelo menos uma raíz entre $1.0$ e $1.5$.

Ainda, considerando essa mesma função, podemos verificar a existência de uma única raíz no intervalo $[1.0, 1.5]$ plotando seu gráfico

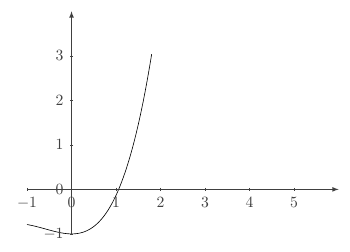
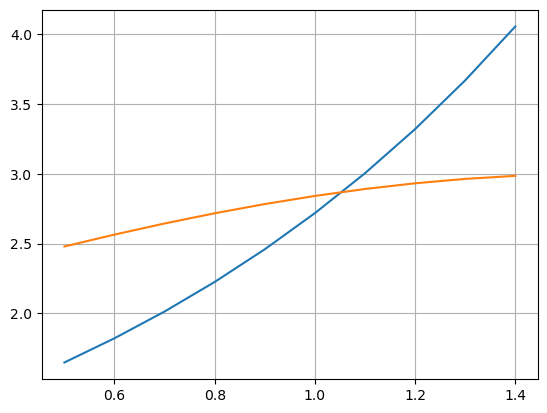
Em Python, podemos plotar os gráficos de $f_1(x)=e^x$ e $f_2(x)=sen(x)+2$ usando o seguinte script:

x = np.arange(0.5, 1.5, 0.1)

f1 = lambda x: np.exp(x)
f2 = lambda x: np.sin(x)+2

plt.plot(x, f1(x), x, f2(x))
plt.grid()
plt.show()

../_images/1db0e81475a0454f532537fe5604f0892fd2773e1300fd3030ae0f2004ded703.png

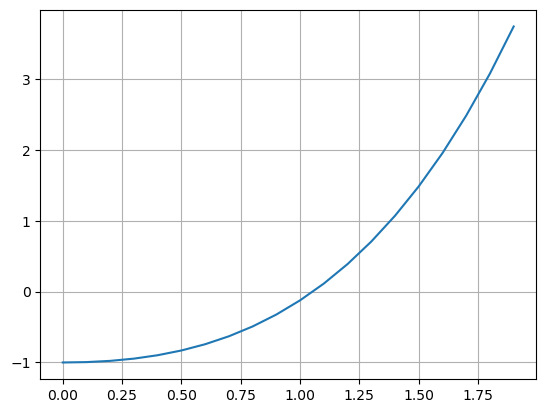
Ou, então, plotar apenas o gráfico de $f(x)=e^x - sen(x) -2$ usando o seguinte script:

x = np.arange(0.0, 2.0, 0.1)

f = lambda x: np.exp(x)-np.sin(x)-2

plt.plot(x, f(x))
plt.grid()
plt.show()

../_images/9cc07f060c9c7bbda192b2fed53d1fabe14399163953cf6d24125917e39a90ea.png

Localização de raízes de polinômios#

Desejamos, localizar as raízes $\overline x$ tal que $P(\overline x) = 0$, em que $P(x)$ é um polinômio de grau $n \in N$, com coeficientes reais ou complexos na forma:

\[P(x)=a_0+a_1 x+a_2 x^2+\cdots+a_n x^n\]

e $a_n \neq 0$.

As raízes de tais polinômios seguem estas regras:

Para uma equação de grau $n$, existem $n$ raízes reais ou complexas. Deve-se observar que essas raízes não serão necessariamente distintas.
Se $n$ for ímpar, existe pelo menos uma raiz real.
Se existirem raízes complexas, elas existem em pares conjugados (isto é, $a+b i$ e $a-b i)$ onde $i=\sqrt{-1}$.

No caso de polinômios, o valor da função pode ser calculado de forma mais eficiente se pensarmos na sequência de operações necessárias quando o polinômio é colocado na forma estruturada, usando parênteses aninhados. Por exemplo, o polinômio de terceiro grau

\[ f_3(x)=a_3 x^3+a_2 x^2+a_1 x+a_0 \]

exige seis multiplicações e seis adições. Em geral um polinômio de grau $n$ exige $n(n+1) / 2$ multiplicações e $n$ adições para ser avaliado em um determinado ponto. Já se ele for reescrito como
$$f_3(x)=\left(\left(a_3 x+a_2\right) x+a_1\right)x+a_0$$

então, requer três multiplicações e três adições.

Exemplo 2.1.8: Considere o polinômio $f(x)=0,8x^5 - 1,3x^4 +5x^3 +17x^2 + 1.9x +10$. Vamos calcular $P(0.5)$ usando um laço simples em que cada passo efetuamos uma multiplicação e uma soma.

a = [0.8, -1.3,5, 17,1.9,10]
x = 0.5; p = 0; dp = 0

for n in range(6):
    p = p*x+a[n]
print(p)

15.76875

Observe que a derivada pode ser obtida incluindo a linha df = df*x+pno laço acima.

p = 0; dp = 0
for n in range(6):
    dp = dp*x+p
    p = p*x+a[n]
print(p, dp)

15.76875 22.25

Verificando os resultados

p = 0.8*x**5-1.3*x**4+5*x**3+17*x**2+1.9*x+10
df = 5*0.8*x**4-1.3*4*x**3+3*5*x**2+2*17*x+1.9
print (p, df)

15.76875 22.25

Observação: Seja $P(x)$ um polinômio de grau $n \geq 1$. Dizemos que $\bar{x}$ é uma raiz de multiplicidade “ $m$ “ da equação $P(x)=0$ se:

\[ P(\bar{x})=P^{(1)}(\bar{x})=\ldots=P^{(m-1)}(\bar{x})=0 \quad \mathrm{e} \quad P^{(m)}(\bar{x}) \neq 0 \]

em que $P^m(\bar{x})$ é a $m$-ésima derivada de $P(x)$ calculada no ponto $\bar{x}$.

Por exemplo, considere o polinômio $P(x)=x^3$. A raiz $\bar{x}=0$ é uma raiz de multiplicidade três da equação $P(x)=0$, pois:

\[ P(x)=P^{(1)}(\bar{x})=0, \quad P^{(2)}(\bar{x})=0 \quad \text { e } \quad P^{(3)}(\bar{x})=6 \neq 0 \]

Entendemos, neste caso, que a equação $P(x)=x^3=0$ possui três raízes idênticas, ou uma raiz de multiplicidade 3 .

A seguir apresentamos alguns teoremas que podem ser utilizados para investigar a localização das raízes de polinômios.

Teorema: Localização de raízes no círculo

Sejam $P(x)=a_0 x^n + a_1 x^{n-1}+...+a_{n-1}x+a_n$ e $A=max\{\left|a_1 \right|,..., \left|a_n \right|\}$. Então, o módulo de todas as raízes $x_k$ , $k = 1,... , n$ satisfaz a inequação:

\[ |x_k|< 1 +\frac{A}{\left|a_0 \right|} = R\]

Para a demonstração, ver Arenales e Darezzo, 2016.

Como consequência desse teorema, tem-se o seguinte corolário:

Sejam $a_n\neq 0$ e $B=max\{\left|a_0 \right|,...,\left|a_{n-1}\right|\}$, em que $a_k$,$k=0,...,n$ são os coeficientes de $P(x)$. Então, o módulo de todas as raízes $x_k$, $k = 1,..., n$ satisfaz a inequação:

\[ \left|x_k \right| > \frac{1}{1+\frac{B}{\left|a_n \right|}}=r\]

(Para a demonstração, ver Arenales e Darezzo, 2015, p 123)

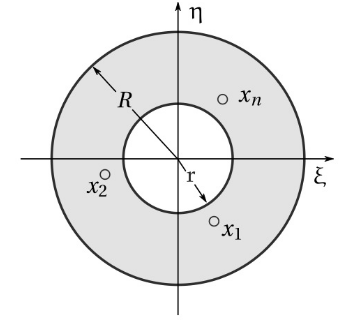
Exemplo 2.1.9: (Fonte: Arenales e Darezzo, 2016) As raízes de $P(x)=x^3+2x^2-x-2=0$ estão localizadas em $-3<x_k< -1/2$ ou $1/2< x_k <3$, pois:

$ |x_k|<1-\frac{2}{|1|} = 3 = R$ e $|x_k|> \frac{1}{1+\frac{2}{|-2|}} = 1/2 = r$

De fato, as raízes de $P(x) = 0$ são dadas por $x = 1$, $x = −1$ e $x = −2$.

Assim, no plano complexo as raízes de $P(x) = 0$ estão localizadas no anel $r < |x| < R$ como ilustra a figura abaixo.

Teorema: regra de sinais de Descartes

Dada uma equação polinomial com coeficientes reais, o número de raízes reais positivas $p$ dessa equação não excede o número $v$ de variações de sinais dos coeficientes. Ainda mais, $(v − p)$ é inteiro par, não negativo.

Para determinar o número de raízes negativas, basta calcular o número de variações de sinais no polinômio $P(−x)$.

Teorema: Budan-Fourier

Se os números $a$ e $b(a<b)$ não são raízes da equação $P(x)=0$, então o número $N(a, b)$ de raízes reais da equação $P(x)=0$ localizadas entre $a$ e $b$ é dado por $N(a, b)=\Delta \bar{N}-2 k \quad(k$ natural $)$, sendo $\Delta \bar{N}=\bar{N}(a)-\bar{N}(b)$ em que $\bar{N}(x)$ é igual ao número de variações de sinais na sequência de sucessivas derivadas:

\[ P(x), P^{(1)}(x), \ldots, P^{(n-1)}, 1 \]

Exemplo 2.1.10: (Fonte: Arenales e Darezzo, 2016) Considere o polinômio $P(x)=x^3+2 x^2-x-2$. Aplicando o teorema de Budan-Fourier, vemos que os valores 3 e -3 não são raízes de $P(x)=0$, pois $P(3)=40$ e $P(-3)=-8$. Desta forma, é possível calcular o número de raízes localizadas em $[-3,3]$ :

Seja $P^{(i)}(x) \rightarrow i$-ésima derivada de $P(x)$. Assim, temos:

\[\begin{split} \begin{array}{rrr} P(3)=40 & P^{(1)}(3)=38 & P^{(2)}(3) \\ P(-3)=-8 & P^{(1)}(-3)=14 & P^{(2)}(-3) \end{array} \end{split}\]

Logo,

\[\begin{split} \begin{gathered} \bar{N}(3)=0 \quad \text { e } \quad \bar{N}(-3)= 3\\ \Delta \bar{N}=\bar{N}(-3)-\bar{N}(3)=3-0 = 3\\ N(-3,3)=3-2 k, \quad k=0,1 \end{gathered} \end{split}\]

Portanto, temos uma ou três raízes no intervalo Pela regra de sinais de Descartes, observamos que a equação possui uma raiz positiva e, portanto, a equação pode ter duas raízes no intervalo $(-3,0)$ ou não ter nenhuma raiz real negativa.

Exercícios:

1. Localize graficamente e determine uma aproximação para as raízes reais das funções dadas.

a) $f(x) = –0.5x^2 + 2.5x + 4.5$

b) $f(x) = 5x^2 – 5x^2 + 6x -2$

c) $f(x) = –25 + 82x – 90x^2 + 44x^3 – 8x^4 + 0.7x^5$

d) $f(x) = – 12 – 21x + 18x^2 – 2.75x^3$

2. Determine um intervalo pequeno (de tamanho 0.1, por exemplo) que contenha as raízes reais das funções dadas.

a) $f(x)=3x-e^x=0$

b) $f(x)=\operatorname{sen}(x)+x^2+1=0$

c) $f(x)=\operatorname{sen}(x)-x+2=0$

d) $f(x)=2 x-\operatorname{tg}(x)=0$

e) $f(x)=3 x-\cos (x)+1=0$

f) $f(x)=\ln (x)-\operatorname{sen}(x)=0$

3. Localize as raízes dos seguintes polinômios:

a) $P(x) = x^3-7x^2+14x-6=0$

b) $P(x) = –25 + 82x – 90x^2 + 44x^3 – 8x^4 + 0.7x^5$

c) $P(x) = – 12 – 21x + 18x^2 – 2.75x^3$

4. (Fonte) Uma gamela de comprimento $L$ tem seção transversal semicircular com raio $r$ (veja a figura abaixo). Quando a gamela está cheia com água até uma distância $h$ do topo, o volume $V$ de água é

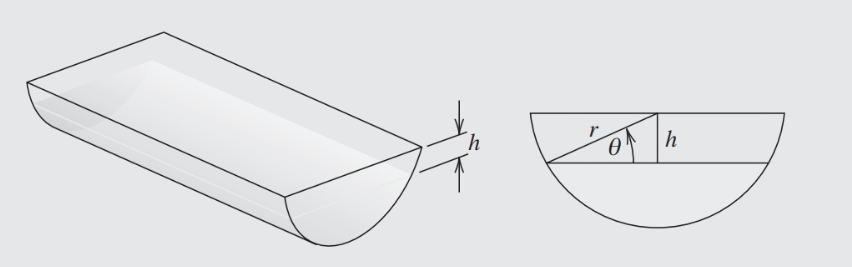
\[ V=L\left[0,5 \pi r^2-r^2 \operatorname{arcsen}(h / r)-h\left(r^2-h^2\right)^{1 / 2}\right] . \]

Suponha que $L=10 pés$, $r= 1$ pé e $V= 12,4$ pés$^3$. Encontre uma aproximação para a profundidade da água na gamela (sem resolver a equação).

5. (Fonte) Uma partícula começa a se movimentar sobre um plano inclinado liso cujo ângulo $\theta$ está variando com velocidade constante

\[ \frac{d \theta}{d t}=\omega<0 . \]

Depois de $t$ segundos, a posição do objeto é dada por

\[ x(t)=-\frac{g}{2 \omega^2}\left(\frac{e^{\omega t}-e^{-\omega t}}{2}-\operatorname{sen} \omega t\right) . \]

Suponha que a partícula tenha se deslocado 1,7 pé em 1 segundo. Obtenha uma aproximação para a velocidade $\omega \operatorname{com}$ a qual $\theta$ varia. Suponha que $g=32,17$ pés $/ \mathrm{s}^2$.

2.1 Localização de raízes

Contents

2.1 Localização de raízes#

Localização por métodos métodos gráficos#

Localização de raízes de polinômios#