4.1. Intepolação polinomial e fórmula de Lagrange#
A interpolação polinomial é um método de aproximação de funções por polinômios. A interpolação é utilizada quando se conhece apenas alguns pontos da função ou quando a função é muito complicada e difícil de manejar. Os polinômios têm a vantagem de serem fáceis de derivar e integrar. Além disso, é possível provar que qualquer função contínua pode ser arbitrariamente aproximada por um polinômio (teorema de Weierstrass).
Outra particularidade é que o valor numérico de um polinômio
para algum valor real de \(x\) pode ser calculado com um número reduzido de operações aritméticas escrevendo-o na forma
o que apresenta algumas vantagens computacionalmente, como veremos mais para frente ao realizar a interpolação pela fórmula de Newton.
Interpolar uma função \(f(x) = y\) em um conjunto de \(n+1\) pontos distintos \({x_0,x_1,...,x_n}\) de um intervalo \([a,b]\) por um polinômio de significa encontrar \(P_n(x)= a_0 + a_1x+...+ax^n\) tal que \(P(x_i)=y_i\) com \(i = 0,1,...,n\). Ou seja, significa encontrar o polinômio de grau \(n\) que “passa” por esses pontos.
Na figura abaixo é mostrada um polinômio que interpola uma função a partir de 6 pontos. É possível observar que o polinômio passa pelos pontos, ou seja, \(P(x_i) = y_i\), \(i=0,1,...,5\), e que aproxima a função razoavelmente bem a função no intervalo de \(x_1\) até \(x_5\). No intervalo entre \(x_0\) e \(x_1\) a aproximação não é tão boa e fora do intervalo \((x_0,x_5)\) parece não funcionar muito bem.

O caso mais simples de interpolação que podemos analisar é o de encontrar a reta (polinômio de grau 1) que passa por dois pontos, \((x_0, y_0)\) e \((x_1,y_1)\). Nesse caso, o polinômio tem a forma \(P(x)=a_0+a_1x\) e para determiná-lo basta encontrar os coeficientes \(a_0\) e \(a_1\) da única reta que passa por esses dois pontos. Logo, os coeficientes podem ser obtidos resolvendo o sistema linear:
\(\begin{cases} y_0 = a_0 + a_1 x_0\\ y_1 = a_0 + a_1 x_1\\ \end{cases} \quad\) ou, na forma matricial \(\quad \left[\begin{array}{cc} 1 & x_0 \\ 1 & x_1 \\ \end{array} \right] \left[\begin{array}{c} a_0 \\ a_1 \\ \end{array} \right]\) \(=\) \(\left[\begin{array}{c} y_0 \\ y_1 \\ \end{array} \right]\)
A solução pode ser obtida fazendo \(a_1 = \frac{y_1 - y_0}{x_1 - x_0}\) e \(a_0 = y_0 - a_1x_0\).
Exemplo 4.1.1:
Vamos obter o polinômio que interpola os pontos \({(1,2),(5,1)}\).
Solução:
Para isso, resolvemos o sistema linear
$\( \begin{cases}
a_0 + a_1 = 2\\
a_0 + 5a_1 = 1\\
\end{cases} \)$
que nos fornece:
\(a_1=\frac{y_1 - y_0}{x_1 - x_0}=\frac{1 - 2}{5 - 1}=-\frac{1}{4}\) e \(a_0 = y_0 - a_1x_0 = 2 +\frac{1}{4} = \frac{9}{4}\)
Assim, obtemos
A figura abaixo mostra o resultado

Assim, generalizando o caso anterior, para obter os coeficientes do polinômio \(P(x)=a_0 + a_1x + a_2x^2+...+a_nx^n\), de grau \(n\), que interpola uma função a partir de \(n+1\) pontos \((x_i,y_i)\), \(i=0,1,...,n\), podemos resolver o seguinte sistema
\(\left[\begin{array}{ccccc} 1 & x_0 & x_0^2 & ... & x_0^n\\ 1 & x_1 & x_1^2 & ... & x_1^n\\ ...& ... & ... & ... & ...\\ 1 & x_n & x_n^2 & ... & x_n^n\\ \end{array} \right] \left[\begin{array}{c} a_0 \\ a_1 \\ ...\\ a_n \\ \end{array} \right]\) \(=\) \(\left[\begin{array}{c} y_0 \\ y_1 \\ ...\\ y_n \\ \end{array} \right]\)
A matriz \(n \times n\) mostrada acima é chamada matriz de Vandermonde e tem determinante não nulo para pontos \(x_i\) distintos, ou seja, polinômio de coeficientes \(a_0,a_1,...,a_n\) existe e é único. Usando o módulo polynomial de Numpy a matriz de Vandermonde pode ser obtida usando a função np.polynomial.polynomial.polyvander.
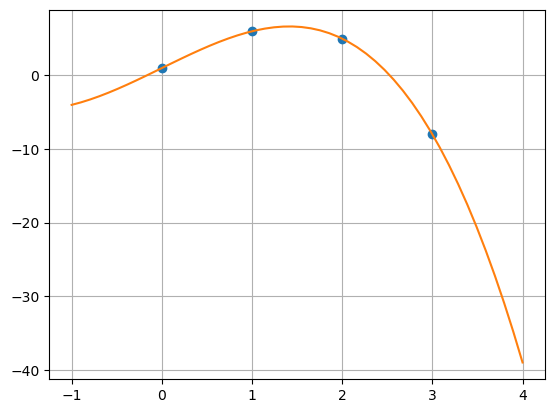
Exemplo 4.1.2: Considere o problema de encontrar um polinômio interpolador para do conjunto de pontos \(\{(0, 1)\), \((1, 6)\), \((2, 5)\), \((3, -8)\}\). Como o conjunto consiste de 4 pontos, o polinômio interpolador deve ser da forma: \(p(x) = a_0 + a_1x + a_2x^2 + a_3x^3\)
O que nos leva ao sistema linear:
cuja solução é \(a_0=1\), \(a_1=6\), \(a_2=0\) e \(a_3=-1\). Portanto, o polinômio interpolador é \(p(x)=1+6x-x^3\).
Podemos verificar o resultado plotando os pontos e o polinômio:
import matplotlib.pyplot as plt
import numpy as np
xi = np.array([0.,1.,2.,3.])
yi = np.array([1.,6.,5.,-8.])
x = np.linspace(-1,4)
y = 1+6*x-x**3
plt.plot(xi,yi,'o',x,y)
plt.grid()
plt.savefig('imagens/Exemplo3.2.png',dpi=300)
Computacionalmente, podemos resolver esse exemplo como é mostrado a seguir, utilizando as operações vetorizadas da biblioteca numpy para montar a matriz do sistema e a função solve do módulo linalg para resolver, assim obtemos facilmente os coeficientes do polinômio interpolador. Também podemos usar a conveniente função polyval para avaliar o valores do polinômio em um conjunto de valores de \(x\). Faremos isso para verificar se correspondem aos valores da função, como é esperado, ou seja, se \(P(x_i)=y_i\), \(i=0,1,2,3\).
A = np.array([xi**0,xi**1,xi**2,xi**3]).T
#ou A = np.polynomial.polynomial.polyvander(xi,3)
ai = np.linalg.solve(A,yi)
coeffs = np.flipud(ai) # reverte a ordem
print ("Coeficientes:", coeffs)
print ("P(xi):", np.polyval(coeffs,xi))
Coeficientes: [-1.00000000e+00 1.33226763e-15 6.00000000e+00 1.00000000e+00]
P(xi): [ 1. 6. 5. -8.]
Como é possível notar, com poucas linhas de código, utilizando as convenientes funções disponíveis na biblioteca NumPy, é possível obter o polinômio que interpola os pontos dados. Podemos também verificar que os numéricos do polinômio em cada um dos pontos coincidem com os valores da função, ou seja, \(f(x_i)\), \(i=0,1,2,3\).
Embora sempre seja possível obter o polinômio interpolador de grau que passa por um conjunto de pontos distintos resolvendo um sistema linear, essa pode não ser a maneira mais eficiente de fazer isso. A seguir serão apresentadas duas fórmulas bem conhecidas para interpolação polinomial que requerem menos esforço computacional, as fórmula de Lagrange e de Newton. A primeira requer um número maior de operações aritméticas básicas mas ainda assim pode ser mais vantajosa quando várias funções precisam ser interpoladas no mesmo conjunto de pontos.
Fórmula Interpolatória de Lagrange#
Seja \(f(x)\) definida em \(x_0, x_1,...,x_n\), \((n+1)\) pontos distintos de um intervalo \([a,b]\) e \(y_i=f(x_i)\), \(i=0,1,...,n\), então o polinômio interpolador de Lagrange é dado por
com
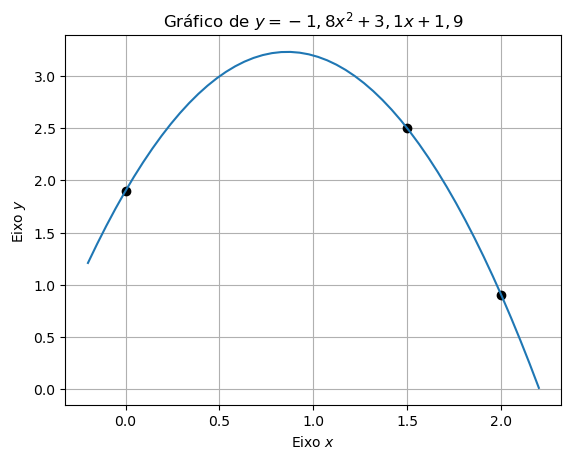
4.1.3: Considere a função \(f(x)\) definida nos pontos \(\{(0.0, 1.9), (1.5, 2.5), (2.0, 0.9)\}\). Determine o polinômio interpolador, usando a fórmula de Lagrange, e estime \(f(0.9)\).
Solução: Queremos o polinômio na forma \(P(x) = y_0 L_0(x) + y_1 L_1(x) + y_2 L_2(x)\). Então, obtemos os \(L_k(x)\) fazendo
\(L_0 = \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} = \frac{(x-1,5)(x-2,0)}{(0,0-1,5)(0,0-2,0)} = \frac{x^2 - 3,5x + 3,0}{3,0}\)
\(L_1 = \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}=\frac{(x-0,0)(x-2,0)}{(1,5-0,0)(1,5-2,0)}=\frac{x^2-2x}{-0,75}\)
\(L_2 = \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}=\frac{(x-0,0)(x-1,5)}{(2,0-0,0)(2,0-1,5)}=\frac{x^2-1,5x}{1,0}\)
Assim, \(P(x)=1,9 \left(\frac{x^2 - 3,5x + 3,0}{3,0}\right) + 2,5 \left( \frac{x^2-2x}{-0,75}\right) + 0.9 \left( \frac{x^2-1,5x}{1,0}\right) = -1,8x^2 - 3,1x + 1,9\)
Portanto, tem-se
\(P(0.9) = -1,8(0,9)^2 + 3,1(0,9) + 1,9 = 3,2320\).
O script Python abaixo plota o gráfico do polinômio obtido juntamente com os pontos tabelados.
import matplotlib.pyplot as plt
import numpy as np
x = [0.0, 1.5, 2.0]
y = [1.9, 2.5, 0.9]
def P(x):
return -1.8*x**2+3.1*x+1.9
xi= np.linspace(-0.2, 2.2)
plt.plot(x, y, 'ko', xi, P(xi),'C0-')
plt.title('Gráfico de $y=-1,8x^2+3,1x+1,9$')
plt.ylabel('Eixo $y$')
plt.xlabel('Eixo $x$')
plt.grid()
plt.savefig('figura_3.3a.png', dpi=300)
No código abaixo é mostrada uma função que calcula o valor numérico do polinômio interpolador usando a fórmula de Lagrange para um dado valor de x. Usando essa função vamos calcular o valor de \(P(9)\) e, também, fazer um laço de repetição para calcular o calor do polinômio em um conjunto de pontos para construir o gráfico. Observe que, como é esperado, o gráfico é igual ao do polinômio que foi obtido analiticamente no exemplo 3.3.
def calculaP(x,X,Y):
valor = 0
for k in range(len(X)):
lk = 1.0
for i in range(len(X)):
if k != i:
lk = lk*(x - X[i])/(X[k]-X[i])
valor = valor + Y[k]*lk
return valor
xp = np.linspace(xi[0], xi[-1])
yp = []
for x in xp:
y = calculaP(x, xi, yi)
yp.append(y)
plt.plot(xi, yi, 'o', xp, yp,'-',color='black')
plt.grid()
plt.show()
print ("P(",0.9,") =", calculaP(0.9, xi,yi))
plt.savefig('figura_3.3a.png', dpi=300)
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
Cell In[6], line 4
2 yp = []
3 for x in xp:
----> 4 y = calculaP(x, xi, yi)
5 yp.append(y)
7 plt.plot(xi, yi, 'o', xp, yp,'-',color='black')
Cell In[5], line 8, in calculaP(x, X, Y)
6 if k != i:
7 lk = lk*(x - X[i])/(X[k]-X[i])
----> 8 valor = valor + Y[k]*lk
9 return valor
IndexError: index 4 is out of bounds for axis 0 with size 4
Exemplo 4.1.4: Considere a função \(f(x)= \frac{0,2x^2sen(x)}{ln\left[(1+x)^2 \right]}\) definida em seis pontos igualmente espaçados tais que \(x_0=0.5\) e \(x_5=5.5\). Vamos usar a função do exemplo 3.3 para plotar o gráfico do polinômio interpolador de Lagrage juntamente com o gráfico da função e os plontos utilizados.
f = lambda x:(0.2*x**2*np.sin(x))/np.log((1 + x)**2)
xi = np.linspace(0.5,5.5,6)
yi = f(xi)
xp = np.linspace(0.1, 6)
yp = []
for x in xp:
y = calculaP(x, xi, yi)
yp.append(y)
plt.plot(xi, yi, 'o',
xp, yp,'-',
xp,f(xp),'--',color='black')
plt.grid()
plt.show()
Fórmula interpolatória de Lagrange para pontos equidistantes#
Se os pontos \(x_0, ..., x_n\) forem igualmente espaçados, ou seja, se \(x_{i+1}-x_i=h\) para \(i=0, ..., n-1\), então é possível fazer uma mudança de variável e obter uma fórmula simplificada para o polinômio interpolador de Lagrange. Fazemos
que é o mesmo que $\( x = x_o +uh\)$
Com essas mudanças, a fórmula de Lagrange fica
com
Para avaliar o valor do polinômio de um determinado valor de \(x\) precisamos obter o valor correspondente na variável \(u\), fazendo, \( u = \frac{x-x_0}{h} \) e calcular \(P(u)\).
Exemplo 4.1.5:
Considere a função \(f(x) = \cos(x)\). Obtenha uma aproximação para \(f(0.3)\) usando um polinômio de grau 2 com \(x_0 = 0.2\) e \(h=0.2\).
def calculaP(u):
valor = 0
for k in range(len(X)):
lk = 1.0
for i in range(len(X)):
if k != i:
lk = lk*(u - i)/(k-i)
valor = valor + Y[k]*lk
return valor
X = np.linspace(0.2, 0.6, 3)
Y = np.cos(X)
h = X[1]-X[0]
u = (0.3 - X[0])/h
print (calculaP(u))
Exercícios:
1. Encontre polinômios interpoladores para as funções (a)\(ln(x+1)\), (b)\(\sqrt{1+x}\) e (c)\(e^{2x}cos(3x)\) no intervalo de \(x_0=1\) até \(x_n=3\) com \(3\), \(4\) e \(5\) pontos escolhidos arbitrariamente no intervalo.
2. Dada a tabela a seguir de valores de uma função \(f\),
x |
0,15 |
0,17 |
0,19 |
0,21 |
0,23 |
0,25 |
0,27 |
0,29 |
0,31 |
|---|---|---|---|---|---|---|---|---|---|
f(x) |
0,176 |
0,234 |
0,278 |
0,322 |
0,361 |
0,398 |
0,431 |
0,462 |
0,491 |
(a) Obtenha uma estimativa para \(f(0,20)\) e para \(f(0,22)\) utilizando interpolação polinomial. (b) Obtenha a expressão analítica do polinômio interpolador. Plote o gráfico. (c) Estime \(f(0,20)\) e \(f(0,22)\) utilizando uma polinomial de terceiro grau. Plote o gráfico e compare com o resultado do item anterior.
3. Considere a função $\(f(x)=\frac{3.21}{0.73 + 9.81x^2}\)$
(a) Aproxime o valor de \(f(1.78)\) usando um polinômio interpolador de grau 3 no intervalo [1, 2] e compare com o valor da função. Mostre o gráfico do polinômio e da função nesse intervalo. (b) Repita o item anterior, mas dessa vez utilize um polinômio de grau 10 no intervalo [-2,2] e comente o que você observou. (c)Pesquise e responda o que é “Fenômeno de Runge”.
4. O concreto novo ganha resistência com o passar dos dias atingindo 99% de sua resistência máxima aos 28 dias. A tabela abaixo mostra os resultados de um ensaio de resistência à compressão simples (em MPa), obtidos em laboratório especializado, de três diferentes traços de concreto:
Dosagem padrão, sem a adição de agregado miúdo reciclado
Substituindo 20% de agregado miúdo natural por agregado miúdo reciclado
Substituindo 40% de agregado miúdo natural por agregado miúdo reciclado.
Dias |
Traço 1 |
Traço 2 |
Traço 3 |
|---|---|---|---|
3 |
14,4025 |
21,8450 |
19,0045 |
7 |
27,4350 |
31,2800 |
26,7450 |
14 |
34,4900 |
35,1600 |
31,3000 |
21 |
34,3750 |
38,1000 |
34,1800 |
28 |
36,1650 |
39,9800 |
35,6550 |
(a) Encontre o polinômio que interpola dos dados de cada um dos ensaios, faça o gráfico. (b) Estime quantos dias são necessários para que cada um dos concretos alcance 32 MPa. (c) Encontre a resistência de cada concreto após 16 dias.
5. Durante três dias consecutivos foi tomada a temperatura (em \(^\circ\)C) numa região de uma cidade, por quatro vezes no período das 6 às 12 horas. Determine, usando todos os dados da tabela abaixo, a média das temperaturas dos três dias às 9 horas.
Hora |
1º dia |
2º dia |
3ºdia |
|---|---|---|---|
6 |
18.5 |
17.2 |
18.1 |
8 |
20.3 |
20.1 |
21.4 |
10 |
24.0 |
25,1 |
22.9 |
12 |
28.2 |
27.5 |
23.7 |
