5.3 Ajuste não linear e linearização

Muitas vezes, temos dados experimentais em que o ajuste como combinação linear nos parâmetros não é adequado e não pode ser considerado. Neste caso, necessitamos de outras famílias de funções para representar adequadamente uma função representada em uma tabela.

Ajuste hiperbólico

Considere os dados obtidos experimentalmente, conforme ilustrado na figura abaixo

Observando a o diagrama de dispersão, vemos que a representação dos dados possui um comportamento do tipo:

\[ g(x) = \frac{1}{a_1x+a_2}\]

Para encontrar os parâmetros \(a_1\) e \(a_2\) da forma como fizemos anteriormente, podemos linearizar a função fazendo

\[ h(x) = \frac{1}{g(x)} = a_1x+a_2 \]

que aproxima a função

\[ \frac{1}{f(x)}\]

e temos agora o caso do ajuste linear, já desenvolvido anteriormente.

Assim, a partir da tabela original, construímos uma nova tabela

\begin{array}{cccc} \hline x_1 &x_2 &… &x_m \ \hline 1/f(x_1) &1/f(x_2) &… &1/f(x_m) \ \hline \end{array}

O problema agora consiste em aproximarmos a função \(\frac{1}{f(x)}\) por uma reta \(h(x)=a_1x+a_2\), e o sistema de equações normais é dado por

\[\begin{split} \begin{cases} \left(\sum_{i=1}^{m}x_i^2\right)a_ 1 +\left(\sum_{i=1}^{m} x_i\right) = \sum_{i=1}^{m} \frac{x_i}{f(x_i)}\\ \left(\sum_{i=1}^{m}x_i\right)a_ 1 +\left(m \right)a_2 = \sum_{i=1}^{m} \frac{1}{f(x_i)}\\ \end{cases} \end{split}\]

Exemplo 1: Considere a função f (x) tabelada nos pontos, como segue

\begin{array}{cccc} \hline x_1 &-3.0 &-2.0 &-1.0 &-0.5 &-0.4 \ \hline f(x_1) &-0.13 &-0.20 &-0.49 &-2.01 &-4.99\ \hline \end{array}

Solução: Plotando os pontos tem-se

import numpy as np
import matplotlib.pyplot as plt

X = np.array([ -3.0, -2.0, -1.0, -0.5, -0.4])
Y = np.array([ -0.13, -0.20, -0.49, -2.01, -4.99])
# plotando
plt.plot(X, Y, "o")
plt.grid()
plt.show()

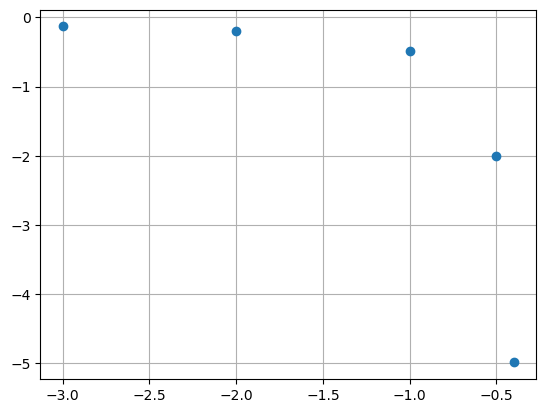
O que sugere um comportamento de uma função do tipo $\(g(x) = \frac{1}{a_1x+a_2}\)\(. Para confirmar, e verificar se a linearização do tipo \)\(h(x) = \frac{1}{g(x)} = a_1x+a_2\)$ irá funcionar, construímos uma nova tabela e plotamos os pontos

Yl = np.power(Y, -1) 
print(Yl)
# plotando
plt.plot(X, Yl, "o")
plt.grid()
plt.show()

[-7.69230769 -5.         -2.04081633 -0.49751244 -0.2004008 ]

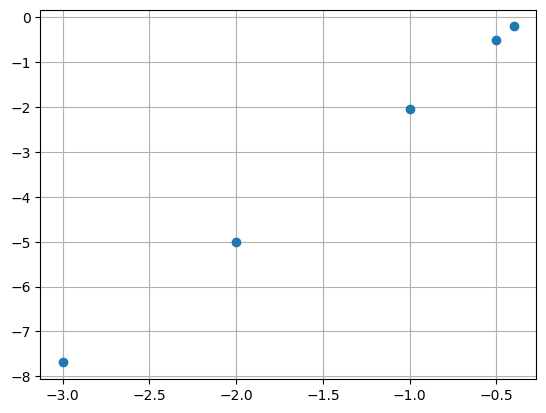
Notamos que os pontos parecem alinhados agora, o que sugere que podemos obter \(a_1\) e \(a_2\) ajustando uma reta a essa nova tabela

# montando a matriz do sistema
A = np.array([[np.sum(X * X), np.sum(X)],
              [np.sum(X),     len(X)]])
B = np.array([np.sum(X*Yl),
              np.sum(Yl)])
# resolvendo
a = np.linalg.solve(A, B)
print ("Parâmetros a1=", a[0]," e a2 =", a[1])

# lista de pontos para os plots
Xr = np.linspace(X[0], X[-1], 50)

#reta
h = lambda X: a[0]*X + a[1]
# plotando
plt.plot(X, Yl, "b.", Xr, h(Xr), "r-") 
plt.grid()
plt.show()

Parâmetros a1= 2.89521778367677  e a2 = 0.9091930898234516

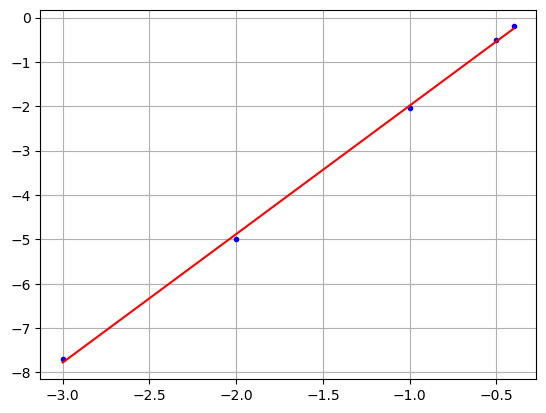
# hipérbole
g = lambda X: np.power(a[0]*X+a[1], -1)
Yr = g(Xr)
# plotando
plt.plot(X, Y, "b.", Xr, g(Xr), "r-") 
plt.grid()
plt.show()

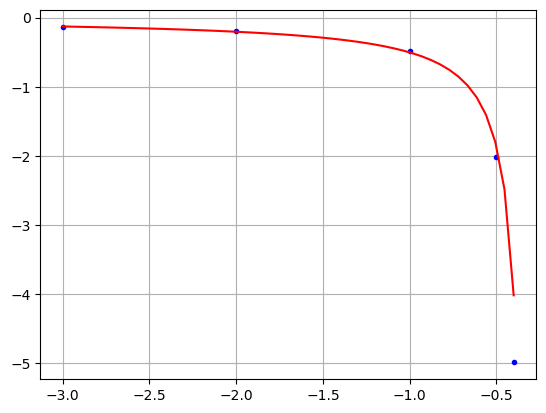
Ajuste exponencial

Podemos obter dados experimentais dispostos conforme ilustrado na figura abaixo, a qual sugere que devemos aproximar a função observada por uma função \(g(x)\) da forma \(g(x) = a(b)^x\) com os parâmetros \(a\) e \(b\) positivos.

O método dos mínimos quadrados desenvolvido anteriormente pode ser usado fazendo-se a seguinte transformação

\[ h(x) = ln(g(x)) = ln(a(b)^x) = ln(a) + xln(b)\]

Então, fazendo

\[ a_1 = ln(a) \to e^{a_1}=a\]

\[ a_2 = ln(b) \to e^{a_2}=b\]

temos a linearização

\[h(x) = a_1 + a_2x\]

Então, construímos ma nova tabela

\begin{array}{cccc} \hline x_1 &x_2 &… &x_m \ \hline ln(f(x_1)) &ln(f(x_2)) &… &ln(f(x_m)) \ \hline \end{array}

e buscamos os parâmetros \(a_1\) e \(a_2\) que ajustam uma reta a esses dados, ou seja, buscamos a solução do sistema

\[\begin{split} \begin{cases} \left(\sum_{i=1}^{m}x_i^2\right)a_ 1 +\left(\sum_{i=1}^{m} x_i\right)a_2 = \sum_{i=1}^{m} ln(f(x_i))x_i \\ \left(\sum_{i=1}^{m}x_i\right)a_ 1 +\left(m \right)a_2 = \sum_{i=1}^{m} ln(f(x_i))\\ \end{cases} \end{split}\]

Exercício resolvido

Exemplo 3: Considere uma função tabelada nos pontos, como segue:

\[\begin{split} \begin{array}{c|c|c|c|c|c|c} x_i & -1 & -0.9 & -0.8 & 0 & 1 & 2 \\ \hline f\left(x_i\right) & 6.01 & 5.39 & 4.80 & 2.01 & 0.65 & 0.21 \end{array} \end{split}\]

Determine uma função \(g(x)\) que melhor se ajuste aos dados da tabela de \(f(x)\).

import math
import numpy as np
from scipy.linalg import solve
import matplotlib.pyplot as plt

X = np.array([ -1, -0.9, -0.8, 0, 1, 2])
Y = np.array([ 6.01, 5.39, 4.8, 2.01, 0.65, 0.21])
Yl = np.log(Y) 

# montando a matriz do sistema
A = np.array([[np.sum(X*X), np.sum(X)],
              [np.sum(X),   len(X)]])
B = np.array([np.sum(X*Yl), np.sum(Yl)])

a = solve(A, B)
print (a)

# lista de pontos para os plots
Xr = np.linspace(X[0], X[-1], 51)
#reta
h = lambda X: a[0]*X + a[1]
# plotando
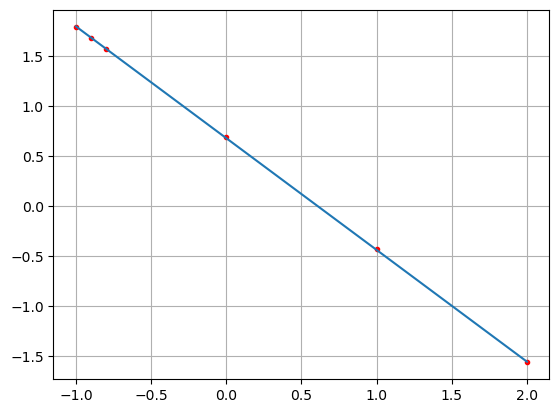
plt.plot(X, Yl, "r.", Xr, h(Xr), "-") 
plt.grid()
plt.show()
  
# hipérbole
k = math.exp(a[1])
b = math.exp(a[0])
g = lambda X: k*np.power(b,X)

Yr = g(Xr)
# plotando
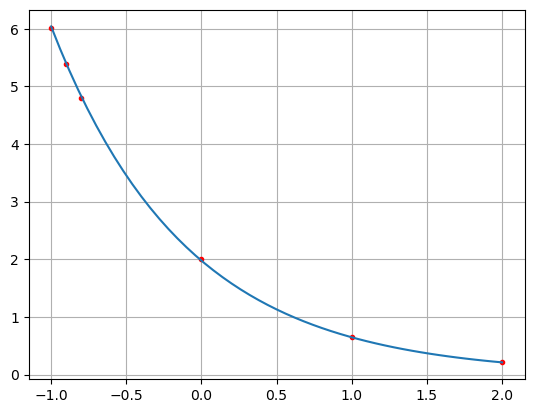
plt.plot(X, Y, "r.", Xr, g(Xr), "-") 
plt.grid()
plt.show()

[-1.11689997  0.68139335]

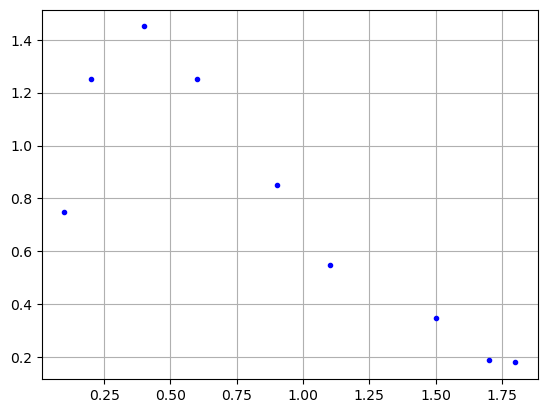
2: Linearize o modelo matemático $\( y = \alpha x e^{\beta x}\)\( e encontre os parâmetros \)\alpha\( e \)\beta\( que fornecem o melhor ajute com base nos seguintes dados. \)\( \begin{array}{cccccccccc} \hline x &0,1 &0,2 &0,4 &0,6 &0,9 &1,1 &1,5 &1,7 &1,8\\ \hline y &0,75 &1,25 &1,45 &1,25 &0,85 &0,55 &0,35 &0,19 &0,18\\ \hline \end{array} \)$

x = np.array([0.1, 0.2, 0.4, 0.6, 0.9, 1.1, 1.5, 1.7, 1.8])
y = np.array([0.75, 1.25, 1.45, 1.25, 0.85, 0.55, 0.35, 0.19, 0.18])
# plotando
plt.plot(x,y, "b.")
plt.grid()
plt.show()

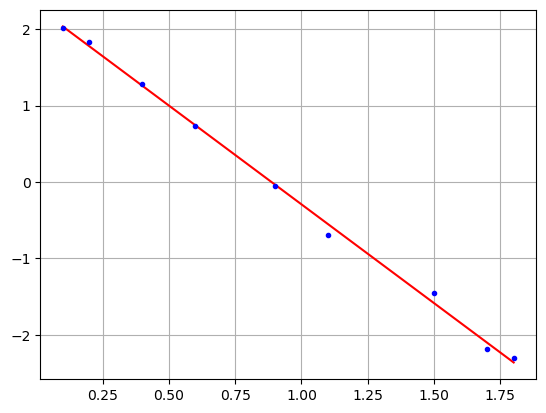
fazendo $\(ln(y)=ln(\alpha x e^{\beta x})\)\( \)\(ln(y)=ln(\alpha)+ln(x)+ \beta x\)\( \)\(ln(y)-ln(x) = \beta x + ln(\alpha)\)$

escrevendo $\(y' = a_1x+a_2\)$

sendo $\(y'=ln(y)-ln(x)\)$

\[a_1 = \beta\]

\[a_2 = ln(\alpha)\]

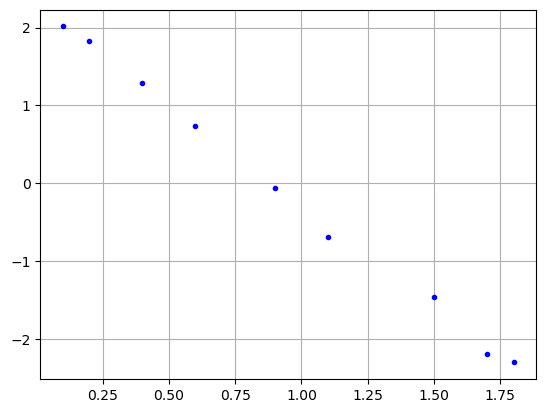
obtemos os pontos alinhados

yl = np.log(y)-np.log(x)
plt.plot(x,yl, "b.")
plt.grid()
plt.show()

A = np.array([[np.sum(x * x), np.sum(x)],
              [np.sum(x),     len(x)]])

B = np.array([np.sum(x*yl),
              np.sum(yl)])

a = solve(A, B)

alpha = np.exp(a[1])
beta = a[0]
print(alpha, beta)

9.910716948702442 -2.58708188621561

h = lambda x: a[0]*x + a[1]

xr = np.linspace(x[0], x[-1], 20)
plt.plot(xr,h(xr), "r-", x,yl, "b.")
plt.grid()
plt.show()

alpha = np.exp(a[1])
beta = a[0]
print(alpha, beta)

9.910716948702442 -2.58708188621561

g = lambda x: alpha*x*np.exp(beta*x) 

xr = np.linspace(0,2, 51) plt.plot(xr,g(xr), “r-”, x,y, “b.”) plt.grid() plt.show()

Resposta: \(\alpha = 9.6618\) e \(\beta = -2.4733\)

Exemplos de linearização de algumas funções:

Exercícios:

1. Considereosdadosdeumexperimentoconformetabela: $\( \begin{array}{c|c|c|c|c|c|c|c} x_i & -9 & -6 & -4 & -2 & 0 & 2 & 4 \\ \hline f\left(x_i\right) & 30.1 & 10.1 & 8.9 & 5.9 & 5.0 & 3.9 & 4.01 \end{array} \)$

Usando o método dos mínimos quadrados e o Software Numérico, ajustar aos dados da tabela funções:

a) Hiperbólica.

b) Exponencial.

c) Compareosresultadosobtidos.

2. Ajuste os dados abaixo (número de bactérias por unidade de volume) à curva \(y=ab^x\). Plote o gráfico da função obtida juntamente com os dados tabelados. $\( \begin{array}{cccccccc} \hline nº de horas &0 &1 &2 &3 &4 &5 &6 \\ \hline nº de bactéricas &32 &47 &65 &92 &132 &190 &275 \\ \hline \end{array} \)$

3. (Fonte) Os dados tabulados a seguir foram gerados a partir de uma experiência que continha inicialmente cianeto de amônio puro (\(NH_4OCN\)). Sabe-se que tais mudanças de concen- tração podem ser modeladas pela seguinte equação:

\[ c=\frac{c_0}{1+k c_0 t} \]

em que \(c_0\) e \(k\) são parâmetros. Use uma transformação para linearizar essa equação. A seguir, use regressão linear para prever a concentração em \(t = 160\) min.

\[\begin{split} \begin{array}{l|ccccc} \mathrm{t}(\mathrm{~min}) & 0 & 20 & 50 & 65 & 150 \\ \hline \mathrm{c}(\mathrm{mols} / \mathrm{L}) & 0,381 & 0,264 & 0,180 & 0,151 & 0,086 \end{array} \end{split}\]

4. (Fonte) O modelo a seguir é usado frequentemente em engenharia ambiental para parametrizar o efeito da temperatura \(T\) (\(°C\)) nas taxas de reações químicas \(k\) (por dia),

\[ k=k_{20} \theta^{T-20} \]

em que \(k_{20}\) e \(\theta\) são parâmetros. Use uma transformação para linearizar essa equação. A seguir, use regressão linear para estimar \(k_{20}\) e \(\theta\) e para prever a taxa de reação em \(T = 17 °C\).

\[\begin{split} \begin{array}{l|ccccc} T\left({ }^{\circ} \mathrm{C}\right) & 6 & 12 & 18 & 24 & 30 \\ \hline k \text { (por dia) } & 0,14 & 0,20 & 0,31 & 0,46 & 0,69 \end{array} \end{split}\]

5. (Fonte) A equação de Andrade foi proposta como um modelo para o efeito da temperatura sobre a viscosidade,

\[ \mu=D e^{B / T_a} \]

onde \(\mu\) é a viscosidade dinâmica da água (\(10^{−3} N · s/m^2\)), \(T_a\) é a temperatura absoluta (\(K\)), e \(D\) e \(B\) são parâmetros. Ajuste esse modelo aos dados para a água

\[\begin{split} \begin{array}{c|cccccc} T & 0 & 5 & 10 & 20 & 30 & 40 \\ \hline \mu & 1,787 & 1,519 & 1,307 & 1,002 & 0,7975 & 0,6529 \end{array} \end{split}\]