1.3 Erros nas aproximações numéricas

1.3 Erros nas aproximações numéricas#

Uma solução numérica é geralmente uma solução aproximada, não exata. A diferença entre a solução exata e a solução aproximada é chamada de erro e é muitas vezes inerente ao processo. Em problemas reais, erros numéricos raramente podem ser evitados.

Os erros podem ocorrer na fase de modelagem matemática, devido a simplificações e a imprecisão nos dados, quanto na fase de resolução, no processo de conversão de base e devido à limitações da máquina em armazenar um número muito grande de dígitos. Ou também, na aproximação de funções representadas por séries infinitas. Como não é possível realizar a soma infinita, então, as série são truncadas e considera-se apenas um número finito de termos, introduzindo o que chamamos de erro de truncamento.

Sabemos também que o computador realiza operações aritméticas retendo apenas um número um número fixo de algarismos significativos. Números como o \(\pi\), \(e\) ou \(\sqrt{7}\) não podem ser expressos por um número fixo de algarismos, portanto não podem ser representtados exatamente por um computador. Além disso, alguns números que têm representação fracionária finita no sistema decimal, não podem ser representados com exatidão no sistema binário. A discrepância introduzida pela omissão de algarismos significativos é chamada erro de arredondamento.

Arredondamento: Dizemos que um número \(n_r\) na base decimal foi arredondado na posição \(k\) se todos os dígitos de ordem maior que \(k\) forem descartados segundo o seguinte critério:

  • O dígito de ordem \(k\) é acrescido de uma unidade se o de ordem \((k + 1)\) for maior ou igual a metade da base

  • do contrário, o número \(nr\) é representado com os \(k\) dígitos iniciais.

Exemplo 1.3.1:

Consideremos o sistema \( SPF (b, n, exp_{min} , exp_{max}) = SPF (10, 4, -5, 5) \)

a) Se \(a=0,5324 \times 10^3\) e \(b=0,4212 \times 10^{-2}\), então \(a \times b = 0,22424688 \times 10^1\), que é arredondado e armazenado como \(a \times b = 0,2242 \times 10^1 = 2,242\).

b) Se \(a=0,5324 \times 10^3\) e \(b=0,1237 \times 10^{2}\), então \(a + b = 0,54477 \times 10^3\), que é arredondado e armazenado como \(a + b = 0,5448 \times 10^3=544,8\).

Usando Python, podemos reproduzir o os resultados acima fazendo:

#a)
a = 0.5324*10**3
b = 0.4212*10**-2
print('Exato:',a*b)

Exato: 2.2424688

print('Arredondado:',round(0.22424688, 4)*10**1)

Arredondado: 2.242

#b)
a = 0.5324*10**3
b = 0.1237*10**2
print('Exato:',a+b)

Exato: 544.77

print('Arredondado:',round(0.54477, 4)*10**3)

Arredondado: 544.8

Exemplo 1.3.2: Neste exemplo vamos calcular o polinômio \(y=x^3-5x^2+6x+0,55\) em \(x = 1,37\) usando aritmética de ponto flutuante com 3 algarismos significativos. Em seguida, vamos repetir os cálculos expressando \(y\) como \(y = ((x – 5)x + 6)x + 0,55\) e comparar.

x = 1.37
print('x³=',x**3)
print('x²=',x**2)

x³= 2.5713530000000007
x²= 1.8769000000000002

print('5x²=',5*1.88)

5x²= 9.399999999999999

6*x

8.22

y = (0.257 - 0.94 + 0.822 + 0.055)*10
print('Letra a: y=', y)

Letra a: y= 1.94

ye = x**3 - 5*x**2 + 6*x+ 0.55
print('Valor exato: y=',ye)

Valor exato: y= 1.956853

print('Erro letra a:', abs(y-ye))

Erro letra a: 0.016853000000000007

y = round((round((x-5)*x,2)+6)*x,2)+0.55
print('Letra b: y=', y)

Letra b: y= 1.96

print('Erro letra b:', abs(y-ye))

Erro letra b: 0.003147000000000011

Truncamento: Quando representamos uma função utilizando uma série infinita mas considerarmos apenas um número finito de termos na série, dizemos que estamos cometendo um erro de truncamento.

Exemplo 1.3.3: A função exponencial \(e^x\) pode ser representada pela série

\[e^x=\sum_{n=0}^{\infty} \frac{x^n}{n!}.\]

Sabemos que \(e\) é um número irracional e portanto sua representação fracionária têm infinitas casas decimais. Podemos obter uma aproximação para o número \(e\) truncando a série

\[e=\sum_{n=0}^{\infty} \frac{1}{n!} = 1+1+\frac{1}{2}+\frac{1}{3!}+\frac{1}{4!}+...\]

Por exemplo, com 5 termos da série obtemos:

e = 1+1+1/2+1/6+1/24+1/120
print ('Valor aproximado:',e)

Valor aproximado: 2.7166666666666663

import math
print ('Valor "exato":', math.e)

Valor "exato": 2.718281828459045

Use o exemplo 1.3.3 como modelo para resolver o Exercício 1 no final do desta seção.

Erro absoluto#

Definimos erro absoluto por

\[ E_{abs} = \left| a_{ex}-a_{aprox} \right| \]

em que \(a_{ex}\) é o valor exato da grandeza considerada e \(a_{aprox}\) é o valor aproximado da mesma grandeza numérica.

Erro relativo#

Definimos erro relativo por

\[ E_{rel} = \frac{E_{abs} }{\left| a_{ex} \right|} \]

em que \(a_{ex}\) é o valor exato da grandeza considerada e \(a_{aprox}\) é o valor aproximado da mesma grandeza.

Podemos observar que o erro relativo nos fornece mais informações sobre a qua- lidade do erro que estamos cometendo num determinado cálculo, uma vez que no erro absoluto não é levada em consideração a ordem de grandeza do valor calculado, enquanto no erro relativo esta ordem é contemplada.

Quando obtemos uma aproximação numérica por meio de uma sequência convergete \(x_0, x_1, x_2,...,x_k,...\)mas não conhecemos a solução exata, o erro relativo no termo \(k\) pode ser expresso como diferença relativa, dada por

\[ \frac{\left|x_{k-1}-x_k \right|}{\left| x_k \right|} \]

Exemplo 1.3.4: A equação \(f(x)=x^2-a=0\), com \(a>0\), podemos utilizar o seguinte processo iterativo:

\[ x_{n+1}=\frac{1}{2} \left( x_n + \frac{a}{x_n} \right), \,\,\, n=1,2,...\]

A partir de uma aproximação inicial \(x_0\), usamos essa expressão para gerar a sequência de soluções aproximadas \(x_1\), \(x_2\), …

Assim, por exemplo, para calcular aproximações para \(\sqrt{2}\), podemos fazer

\( x_0 = 1.5 \)

\( x_1 = 1/2(1.5 + 2/1.5) = 1.4166666666666665 \)

\(x_2 = 1/2(1.4166666666666665 + 2/1.4166666666666665) = 1.4142156862745097 \)

E assim por diante.

Em Python podemos fazer:

x = 1.0
x_ant = 0.0

err = 10.0

while err>0.0001:
    x = 0.5*(x + 2/x)
    err = abs(x-x_ant)/abs(x)
    x_ant = x
    print (x, err)

1.5 1.0
1.4166666666666665 0.058823529411764816
1.4142156862745097 0.001733102253032923
1.4142135623746899 1.5018239651360762e-06

Usando o exemplo 1.3.4 acima, resolva o Exercício 2 no final da seção.

Exemplo 1.3.5:

A sequência \(x_k = 1+ \frac{1}{x_{k-1}}\) converge para \(\overline{x} = \frac{1+\sqrt{5}}{2}\). Fazendo \(i = 0,1,2,...,10\) e \(x_0 = 1\), mostre a sequência de aproximações juntamente com as diferenças relativas e os erros relativos para cada termo.

import math
x = 1.
x_ant = x
x_exa = (1+math.sqrt(5))/2

for k in range(10):
    x = 1.+1./x
    dif = abs(x-x_ant)/abs(x)
    err = abs(x-x_exa)/abs(x_exa)
    print (x, x_exa, err, dif)
    x_ant = x

2.0 1.618033988749895 0.23606797749978967 0.5
1.5 1.618033988749895 0.07294901687515776 0.3333333333333333
1.6666666666666665 1.618033988749895 0.030056647916491288 0.09999999999999992
1.6 1.618033988749895 0.01114561800016822 0.04166666666666652
1.625 1.618033988749895 0.004305231718579094 0.01538461538461533
1.6153846153846154 1.618033988749895 0.0016374027886314115 0.005952380952380931
1.619047619047619 1.618033988749895 0.0006264579760202099 0.002262443438914019
1.6176470588235294 1.618033988749895 0.0002391358457583512 0.0008658008658008628
1.6181818181818182 1.618033988749895 9.136361346616536e-05 0.00033046926635820254
1.6179775280898876 1.618033988749895 3.48946069117676e-05 0.00012626262626264404

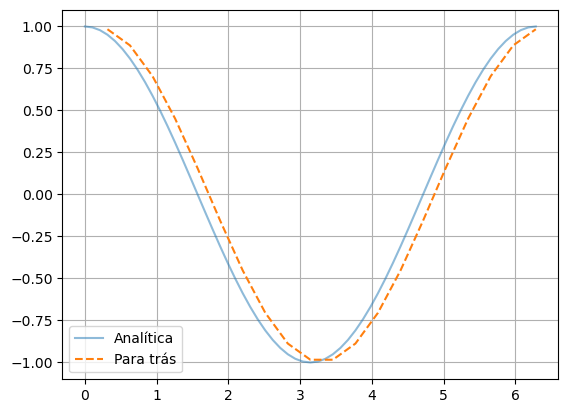
Exemplo 1.3.6: Podemos obter uma aproximação para a derivada primeira de uma função \(y=f(x)\) usando a fórmula:

\[ \frac{dy}{dx} \cong \frac{\Delta y}{\Delta x} = \frac{f(x+\Delta x)-f(x)}{\Delta x} \]

tomando um valor pequeno de \(\Delta x\).

Sabemos que a derivada primeira de \(f(x)=sen(x)\) é \(f'(x)=cos(x)\). Vamos calcular as derivadas numericamente para deversos pontos no intervalo \([0,2\pi]\) e fazer o gráfico.

import numpy as np
import matplotlib.pyplot as plt

xi = np.linspace(0, 2*np.pi, 21)
h=(xi[-1]-xi[0])/(len(xi)-1)
f = lambda x: np.sin(x)

dxi = (f(xi[1:])-f(xi[0:-1]))/h

xplot = np.linspace(0, 2*np.pi, 61)

plt.plot(xplot,np.cos(xplot),'-',
         alpha=0.5,label='Analítica')
plt.plot(xi[1:],dxi,'--',label='Para trás')

plt.grid()
plt.legend()
plt.show()
../_images/a67afc074513ae63aee27c3279f04bb76d95fc1159f401d5d774de6af9602633.png

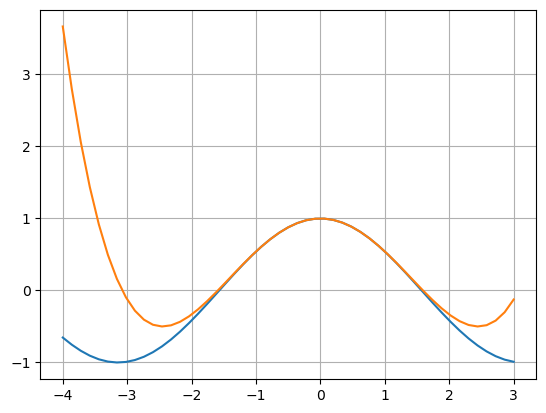
Exemplo 1.3.7: A Série de Taylor é pode ser usada para aproximar funções em torno de um ponto \(a\) truncando a somatória infinita

\[ f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n . \]

Nos códigos a seguir vamos usar a série de Taylor para calcular \(\cos(x)\) e \(e^x\) em um conjunto de pontos e, então, fazer o gráfico dessas funções.

# cos(x)
import numpy as np
import matplotlib.pyplot as plt
import math

X = np.linspace(-4., 3., 51)
print(X)

     
Y = []
#x=1.0
for x in X:   
    valor = 1.0
    for i in range(1,3,1):
        fat = math.factorial(2*i)
        valor = valor + (x**(2*i)*(-1)**i)/fat
        #fat = math.factorial(2*i+1)
        #valor = valor + (x**(2*i+1)*(-1)**i)/fat

        #print (x, valor)
    Y.append(valor)        



plt.plot(X, np.cos(X),X, Y)
plt.grid()
plt.show()

[-4.   -3.86 -3.72 -3.58 -3.44 -3.3  -3.16 -3.02 -2.88 -2.74 -2.6  -2.46
 -2.32 -2.18 -2.04 -1.9  -1.76 -1.62 -1.48 -1.34 -1.2  -1.06 -0.92 -0.78
 -0.64 -0.5  -0.36 -0.22 -0.08  0.06  0.2   0.34  0.48  0.62  0.76  0.9
  1.04  1.18  1.32  1.46  1.6   1.74  1.88  2.02  2.16  2.3   2.44  2.58
  2.72  2.86  3.  ]
../_images/0e560f20b13a44565c2fbb51361d595486689bcb50bba7f382bd9e85f0a4580b.png 
#e^x

X = np.linspace(-2., 2., 21)
#print(X)

Y = []
#x=1.0
for x in X:   
    valor = 1.0
    fat_i = 1.0
    for i in range(1,3,1):
        fat_i = fat_i * i
        valor = valor + (x**i)/fat_i
        #print (x, valor)
    Y.append(valor)        



plt.plot(X, np.exp(X), X, Y)
plt.grid()
plt.show()
../_images/a318cf7f892b54d2900fd985256dabf5ae7a371acb81cdcdb5beb68cb52ec2c4.png

Exercícios#

1. A função seno pode ser representada pela série de Maclaurin, fazendo $\( \text{sen} \, x=\sum_{n=0}^{\infty} \frac{(-1)^n}{(2 n+1)!} x^{2 n+1} \)$

Encontre aproximações para \(\text{sen}(\pi/4)\) com 3, 5 e 20 termos.

2. Usando o exemplo 1.3.4 como referência, encontre o valor de \(\sqrt{3}\) com um erro relativo mentor que \(10^{-5}\). Quantas iterações são necessárias fazendo \(x_0=1\)? O número de iterações diminui se fizermos \(x_0=1.5\)?

3. A função cosseno pode ser representada pela série de Maclaurin, fazendo $\( \cos x=\sum_{n=0}^{\infty} \frac{(-1)^n}{(2 n)!} x^{2 n}. \)$

Descubra quantos termos da série são necessários para obter uma aproximação para \(\cos(\pi/6)\) com erro relativo menor que \(10^{-4}\).

4. Sabendo que a função \(ln(1+x)\) pode ser representada pela série de Maclaurin, fazendo $\( \ln (1+x)=\sum_{n=0}^{\infty} \frac{(-1)^n}{n+1} x^{n+1} \quad \text { para }|x|<1 \)$

Descubra quantos termos da série são necessários para obter uma aproximação para \(ln(0.2)\) com erro relativo menor que \(10^{-4}\).

5. Usando a fórmula mostrada no Exemplo 1.3.6, encontre uma aproximação para a derivada de \(f(x)=2^xsen(x)\) em \(x=1,23\) e calcule o erro relativo.

Contents