2.2. Método da bisseção#
Muitos problemas em ciências e engenharia envolvem a resolução de uma equação que pode ser colocada na forma
Em alguns casos a solução exata \(\overline{x}\) pode ser encontrada por processos analíticos, quando isso não for possível, uma solução aproximada pode ser obtida por métodos numéricos.
Encontrar um solução para equação \(f(x)=0\) por métodos numéricos consiste em gerar uma sequência de soluções aproximadas, a partir de uma aproximação inicial \(x_0\). Caso os valores obtidos pelo processo iterativo estejam se aproximando da solução exata \(\overline{x}\), dizemos que a sequência está convergindo para a solução.
O Método da Bisseção é o método numérico para resolução de equações do tipo \(f(x)=0\), no qual, a partir de um intervalo inicial \([a,b]\) contendo uma única raiz, é gerada uma sequência de subintervalos, dividindo-se, a cada iteração, o intervalo que contém a raiz em dois subintervalos de mesma amplitude. A cada passo, é verificado qual dos dois subintervalos contém a raiz utilizando o teorema de Bolzano (ou Teorema do Valor Intermediário), enunciado abaixo.
Teorema de Bolzano:#
Se \(f(x)\) é contínua em \([a,b]\) e \(f(a)\cdot f(b)<0\), então existe pelo menos uma raíz \( \overline{x} \in [a,b]\) tal que \(f(x)=0\).
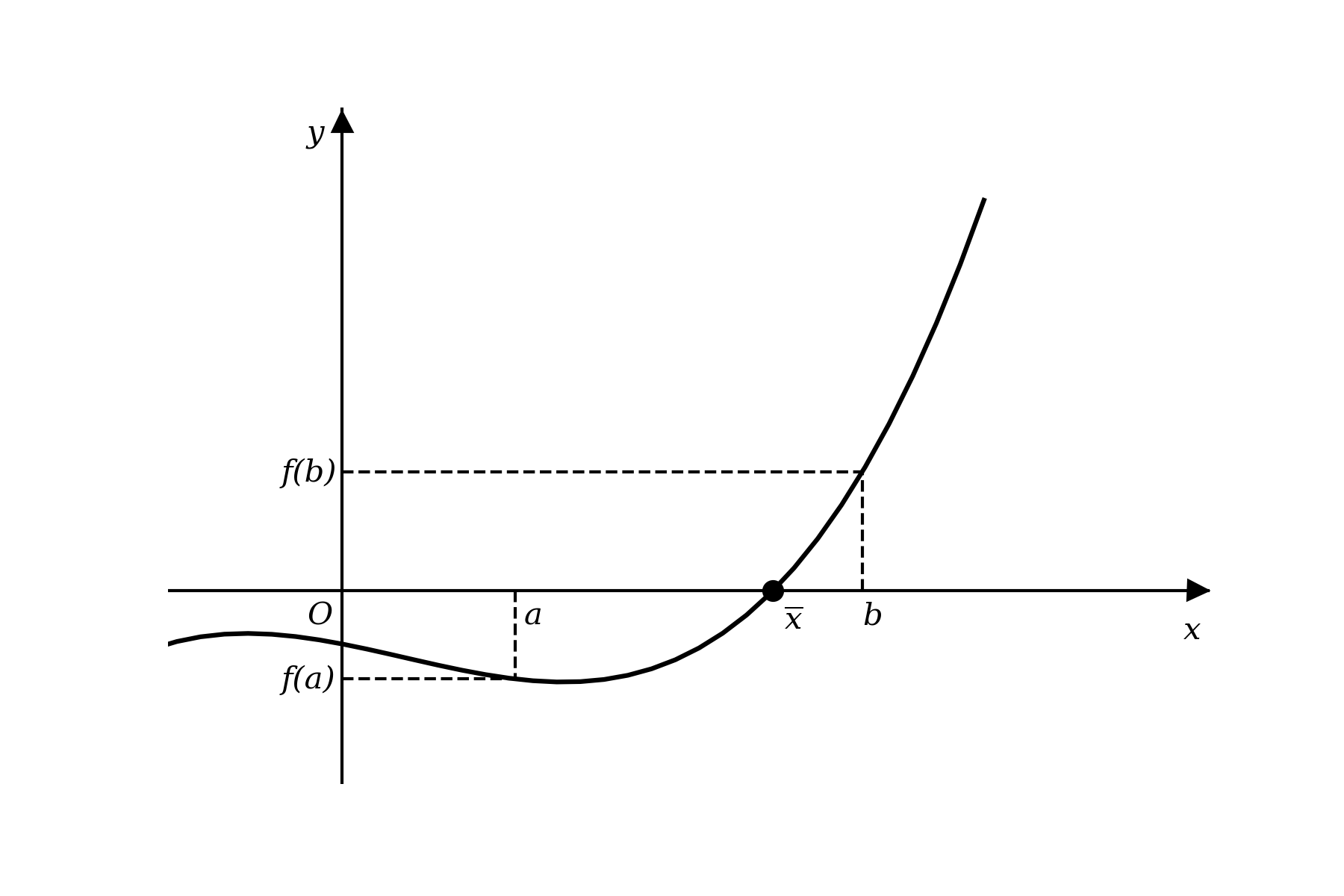
A sequência de subintervalos será calculada até que a amplitude do intervalo obtido menor que uma tolerância pré estabelecida. Assim, podemos descrever o processo no seguinte algoritmo:
Determinar um intervalo inicial \([a,b]\) contendo uma única raíz de \(f\);
Calcular o ponto médio \(x_m=\frac{b+a}{2}\).
Se \(|b-a|>\epsilon\) ou \(E_{rel}<\epsilon\) segue, senão, assumir \(\overline{x}\approx x_m\) e parar;
Se \(f(x_m)=0\), então, a raiz \(\overline{x}\) é o próprio \(x_m\);
Se \(f(a)\cdot f(x_m)<0\) fazemos \(b=x_m\), senão fazemos \(a=x_m\) e voltamos ao passo 2;
Número de iterações#
Podemos estimar o número de iterações necessárias para encontrar a aproximação para a raiz \(\overline{x}\) com a precisão desejada. Considerando que a cada iteração o intervalo é dividido ao meio, então na n-ésima iteração tem-se um intervalo de amplitude \(\frac{b-a}{2^n}\), então, queremos que
ou
que leva a
Assim, \(n\) é o número mínimo de iterações que devem ser realizadas para se obter \(\overline{x}\) com precisão \(\epsilon\).
Exemplo 2.2.1: Usando o método da bisseção, resolva a equação \(x^2+ln(x)=0\), com \(\epsilon = 0.01\).
Solução: Reescrevendo a equação como \(x^2=-ln(x)\) e esboçando os gráficos de \(f_1(x)=x^2\) e \(f_2(x)=-ln(x)\) observamos que existe uma raiz no intervalo \([0.1,1]\).

Então, na primeira iteração fazemos \(x_m = \frac{a+b}{2}=\frac{1.0-0.1}{2}=0.55\). Como \(f(a)=f(0.1)=-2.293\), \(f(b)=f(1.0)=1\) e \(f(x_m)=f(0.55)=-0.295\) temos que a raíz está no intervalo \([x_m,b]\). Além disso, \(\frac{|x_1-x_0|}{|x_0|}=0.2953\) é maior que \(\epsilon = 0.01\). Então seguimos o processo iterativo obtendo a sequên cia abaixo.

Em Python podemos fazer o gráfico como é mostrado a seguir
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [4,3]
f1 = lambda x: x**2
f2 = lambda x: -np.log(x)
xi = np.linspace(0.1, 2, 100)
plt.plot(xi, f1(xi))
plt.plot(xi, f2(xi))
plt.grid()

As iterações para encontrar uma aproximação podem ser obtidas como é mostrado abaixo:
a = 0.1; b = 1.0; err = 10.0; x_ant = 0.0
f = lambda x: x**2 + np.log(x)
for i in range(8):
x = (a+b)/2.0
if f(x)*f(a) < 0:
b = x
else:
a = x
print ("x =", round(x,4))
x = 0.55
x = 0.775
x = 0.6625
x = 0.6063
x = 0.6344
x = 0.6484
x = 0.6555
x = 0.652
Exemplo 2.2.2: Calcular, pelo método da bisseção, corretamente até a terceira casa decimal, a raiz da equação \( \left( \frac{x}{2} \right)^2 -sen(x) = 0 \), localizada no intervalo (\(a_0=1,5\) e \(b_0=2\)).
a = 1.5
b = 2.0
err = 1.0
x_ant = 0.0
def f(x):
y = (0.5*x)**2-np.sin(x)
return y
while err>0.0001:
x = (a+b)/2.0
if f(x)*f(a) < 0:
b = x
elif f(x)*f(a) > 0:
a = x
else:
print ("A raiz exata é x=", x)
break
err = abs(x-x_ant)
x_ant = x
print ("x = %.4f"%x,"| Err = %.4f"% err)
x = 1.7500 | Err = 1.7500
x = 1.8750 | Err = 0.1250
x = 1.9375 | Err = 0.0625
x = 1.9062 | Err = 0.0312
x = 1.9219 | Err = 0.0156
x = 1.9297 | Err = 0.0078
x = 1.9336 | Err = 0.0039
x = 1.9355 | Err = 0.0020
x = 1.9346 | Err = 0.0010
x = 1.9341 | Err = 0.0005
x = 1.9338 | Err = 0.0002
x = 1.9337 | Err = 0.0001
x = 1.9338 | Err = 0.0001
Exemplo 2.2.3: Use o método da bisseção para obter um zero da função \(f(x)=x\log x-1\) com precisão \(\epsilon = 0.01\)
from math import log10
a = 2.0
b = 3.0
err = 1.0
x_ant = a
i = 0
f = lambda x:x*log10(x)-1
while err>0.01:
x = (a+b)/2.0
err = abs(x - x_ant)/abs(x)
print (i, a, b, x, round(f(a),5), round(f(b),5), round(f(x),5), round(err,5))
if f(a)*f(x)<0:
b = x
else:
a = x
i = i+1
x_ant = x
0 2.0 3.0 2.5 -0.39794 0.43136 -0.00515 0.2
1 2.5 3.0 2.75 -0.00515 0.43136 0.20816 0.09091
2 2.5 2.75 2.625 -0.00515 0.20816 0.10021 0.04762
3 2.5 2.625 2.5625 -0.00515 0.10021 0.0472 0.02439
4 2.5 2.5625 2.53125 -0.00515 0.0472 0.02094 0.01235
5 2.5 2.53125 2.515625 -0.00515 0.02094 0.00787 0.00621
Exemplo 2.2.4: Localize e as raízes e use o método da bisseção para obter os zero da função \(f(x)=x^3-9x+3\) com precisão \(\epsilon = 10^{-3}\)
Solução: Nesse exemplo, vamos começar fazendo o gráfico da função.
xi = np.linspace(-5, 5, 21)
f = lambda x: x**3-9*x+3
plt.plot(xi, f(xi))
plt.grid()
plt.show()

Pelo gráfico, podemos ver que parece existirem três raízes distintas \(x_1 \in (-4,-3)\), \(x_2 \in (0, 1)\) e \(x_3 \in (2,3)\). Vamos confirmar criando uma tabela de valores com o código a seguir.
xi = np.linspace(-4,3, 15)
for x in xi:
print (x, f(x))
-4.0 -25.0
-3.5 -8.375
-3.0 3.0
-2.5 9.875
-2.0 13.0
-1.5 13.125
-1.0 11.0
-0.5 7.375
0.0 3.0
0.5 -1.375
1.0 -5.0
1.5 -7.125
2.0 -7.0
2.5 -3.875
3.0 3.0
Pela tabela, confirmamos a existência das raízes nos segintes intervalos: \(x_1 \in (-3.5,-3)\), \(x_2 \in (0, 0.5)\) e \(x_3 \in (2.5,3)\). usaremos agora o método da bisseção para encontrar cada uma das raízes com erro inferior a \(10^{-3}\). Faremos isso criando uma função para o método da bisseção, cujos argumantos de entrada são o intervalo inicial(a,b) e a precisão \(\epsilon\).
def bissec(f, a, b, eps):
err = 100
x_ant = a
while err>0.01:
x = (a+b)/2.0
err = abs(x - x_ant)/abs(x)
if f(a)*f(x)<0:
b = x
else:
a = x
x_ant = x
return (x)
eps = 10**(-3)
print ("x1 =", bissec(f, -3.5, -3, eps))
print ("x2 =", bissec(f, 0, 0.5, eps))
print ("x3 =", bissec(f, 2.5, 3, eps))
x1 = -3.15625
x2 = 0.337890625
x3 = 2.828125
Exercícios#
1. Localize graficamente e determine as raízes reais das funções dadas. Estime o erro relativo a cada iteração e pare quando \(\epsilon \leq 1\% \).
a) \(f(x) = –0.5x^2 + 2.5x + 4.5\)
b) \(f(x) = 5x^2 – 5x^2 + 6x -2\)
c) \(f(x) = –25 + 82x – 90x^2 + 44x^3 – 8x^4 + 0.7x^5\)
d) \(f(x) = – 12 – 21x + 18x^2 – 2.75x^3\)
e) \(f(x)=3x-e^x=0\)
f) \(f(x)=\operatorname{sen}(x)+x^2+1=0\)
g) \(f(x)=\operatorname{sen}(x)-x+2=0\)
h) \(f(x)=2 x-\operatorname{tg}(x)=0\)
i) \(f(x)=3 x-\cos (x)+1=0\)
j) \(f(x)=\ln (x)-\operatorname{sen}(x)=0\)
2. Como mostrado na figura abaixo, a velocidade da água, \(v(m/s)\), descarregada de um tanque cilíndrico através de um cano longo pode ser calculada por
em que \(g=9.81m/s^2\), \(H\) é a altura inicial \((m)\), \(L\) é o comprimento do cano (\(m\)) e \(t\) é o tempo decorrido (\(s\)). Determine a altura necessária para atingir \(v=5m/s\) em \(2.5s\) para um cano de \(4m\) de comprimento pelo método da bisseção e pelo método do ponto-fixo com \(\epsilon = 0.001\)

3. Água está escoando em um canal trapezoidal a uma vazão de Q = 20 m\(^3\)/s. A profundidade crítica \(y\) para tal canal deve satisfazer a equação
onde \(g\) = 9.81 m/s\(^2\), \(A_c\) é a área da seção transversal (m\(^2\)) e \(B\) é a largura do canal na superfície (m). Para esse caso, a largura e a área transversal podem ser relacionadas à profundidade \(y\) por
$B = 3+y \,\,\,\,$ e $\,\,\,\,A_c=3y+\frac{y^2}{2}$
Encontre a profundidade crítica usando o método gráfico da bissecção e itere até que o erro aproximado fique abaixo de 1%. Discuta seus resultados
