6.3 Regra dos trapézios

Consiste am aproximar a integral da função em um intervalo [𝑎,𝑏] pela integral do polinômio de grau 1 que passa pelos pontos (𝑎,𝑓(𝑎)) e (𝑏,𝑓(𝑏)). Se 𝑓(𝑥)>0 em [𝑎,𝑏] a área entre o gráfico da função e o eixo 𝑥 é aproximado pela área do trapézio de altura ℎ=𝑏−𝑎 e bases 𝑓(𝑎) e 𝑓(𝑏).

Considere uma função \(f(x)\) definida nos pontos \(x_0\) e \(x_1\) no intervalo \([a,b]\). O polinômio de Lagrange para esses pontos, considerando a mudança de variável \(u = \frac{x-x_0}{h}\), é dado por

\[P(u) = f(x_0) (1-u) + f(x_1)(u)\]

e a integral pode ser aproximada como segue

\[\int_{x_0}^{x_n} f(x) dx \approx \int_{x_0}^{x_1} P_1(x) dx= h \int_{0}^{1} P_1(u) du\]

ou, ainda,

\[h \int_{0}^{1} P_1(u) du = h \int_{0}^{1} [f(x_0) (1-u) + f(x_1)(u)] du = h f(x_0) \int_{0}^{1} (1-u) du + hf(x_1)\int_{0}^{1} (u) du\]

que resulta em

\[\int_{x_0}^{x_n} f(x) dx \approx \frac{h}{2} [f(x_0)+f(x_1)]\]

ou seja, tem-se aqui a fórmula da área do trapézio.

Graficamente, tem-se

RiemannLeft.png

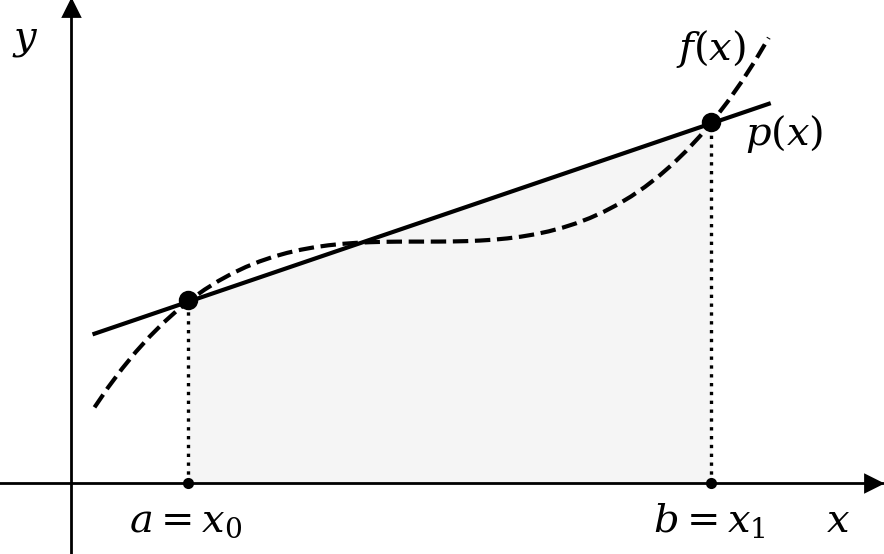Figura 6.3 - Interpretação geométrica da regra dos trapézios

Um limitante superior para o erro será dado por

\[|E_1| \leq \frac{h^3}{12} max.\{|f^{(2)}(x)|, x_0 \leq x \leq x_1 \}\]

A regra dos trapézios repetida (ou generalizada), consiste na subdivisão do intervalo \([a,b]\) em \(n\) subintervalos iguais, de amplitude \(h=\frac{x_n-x_0}{n}\), \(x_0=a\) e \(x_n=b\) e na aplicação da regra dos trapézios repetidamente a cada dois pontos consecutivos.

Assim, temos

\[\int_{x_0}^{x_n} f(x) dx \approx \frac{h}{2} [f(x_0)+f(x_1)] + \frac{h}{2} [f(x_2)+f(x_2)] + ... + \frac{h}{2} [f(x_{n-1})+f(x_n)]=\]

\[= \frac{h}{2} [f(x_0)+ 2f(x_1) + 2f(x_2)+...+2f(x_{n-1})+f(x_n)] =\]

\[= \frac{h}{2} \{f(x_0)+ 2[f(x_1) + f(x_2)+...+f(x_{n-1})]+f(x_n)\}\]

E o limitante superior para o erro será dado por

\[|E_t| \leq \frac{h^2}{12}(x_n-x_0) max.\{|f^{(2)}(x)|, x_0 \leq x \leq x_n \}\]

Exemplo 6.2: Vamos calcular o valor aproximado da integral

\[\int_{1.5}^{5.5} \frac{1}{x}dx\]

usando a regra dos trapézios.

Solução: Basta fazer $\(\int_{1.5}^{5.5} \frac{1}{x} dx \approx \frac{4}{2} [f(1.5)+f(5.5)] = 2 \left( \frac{1}{1.5} + \frac{1}{5.5} \right) \approx 1.697\)$

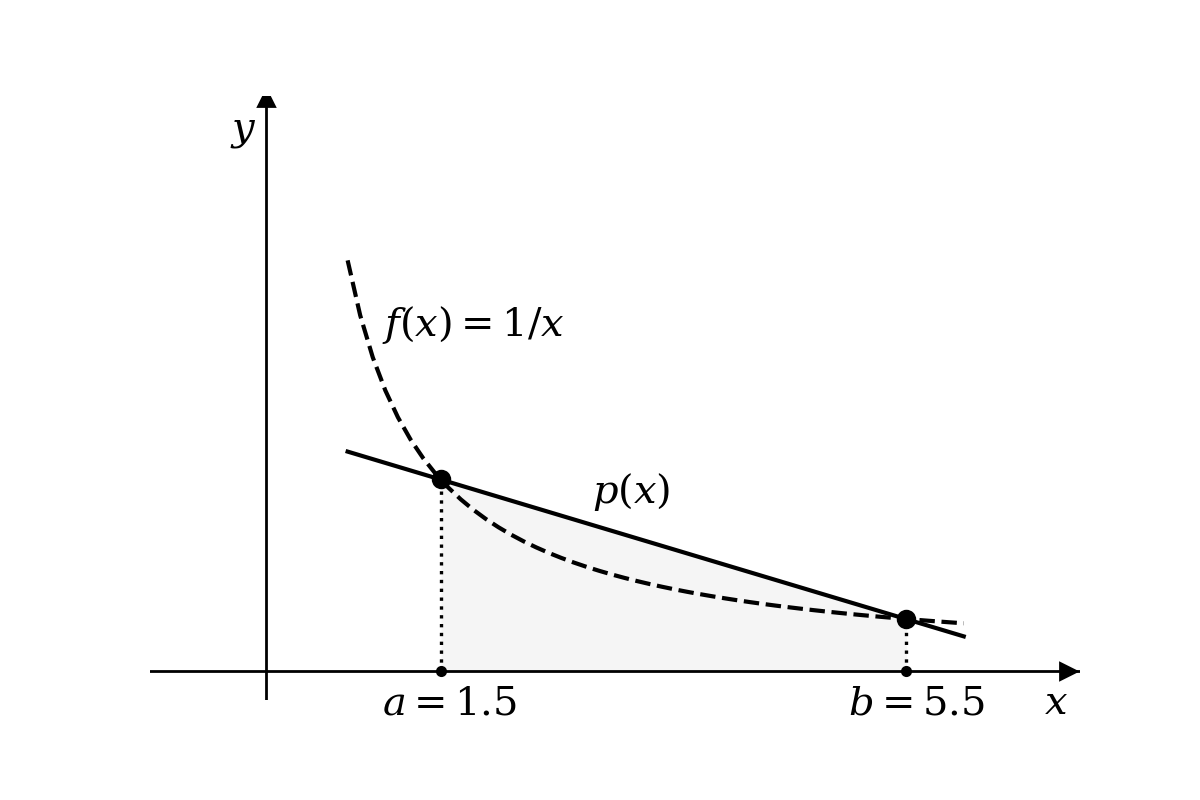
Resolvendo analiticamente o valor exato é \(ln(5.5)\) - \(ln(1.5)\) que pode ser calculado usando uma calculadora obtendo-se \(1.2992829841302609\). O valor obtido pela regra do trapézio é maior, como pode ser verificado observando na figura, comparando-se as áreas. Vamos usar a regra dos trapézios repetida para 5, 10 e 100 subintervalos para ver como fica.

import numpy as np

x0 = 1.5; xn = 5.5 
f = lambda x: 1/x

for n in [5,10,100]:
    h = (xn-x0)/n
    xi = np.linspace(x0, xn, n+1)   
    It = h*((f(xi[0])+f(xi[-1]))/2 + np.sum(f(xi[1:-1])))
    print ("n=",n,", I=",It)

n= 5 , I= 1.3206255135651455
n= 10 , I= 1.304727563368882
n= 100 , I= 1.2993378314867685

A biblioteca numpy já traz uma implementação da regra dos trapézios. Veja como usar no exemplo a seguir com os pontos, o espaçameto e a função definidos acima.

np.trapz(f(xi),dx=h)

1.2993378314867685

A biblioteca scipy também possui funções para integrais definidas. Para saber mais pesquise por scipy.integrate.

Exemplo 6.2: Vamos calcular o valor aproximado da integral

\[\int_1^4 \sqrt{x}dx\]

usando a regra dos trapézios generalizada para 2, 4 e 6 subintervalos e obter um limitante superior para o erro.

f = lambda x: np.sqrt(x)
xi = np.linspace(1, 5, 6)
np.trapz(f(xi), xi)

6.772340295647981

xi = np.linspace(1, 5, 11)
np.trapz(f(xi), xi)

6.78322070363297

xi = np.linspace(1, 5, 101)
np.trapz(f(xi), xi)

6.786856407214704