4.2 Fórmula de Newton#
Seja \(f(x)\) definida em \(x_0, x_1,...,x_n\), (n+1) pontos distintos de um intervalo \([a,b]\) e \(y_i=f(x_i)\), \(i=0,1,...,n\). O polinômio interpolador de Newton é dado por
onde \(f[x_0]\), \(f[x_0,x_1]\),…,\(f[x_0,...,x_n]\) são as diferenças divididas, definidas como é mostrado a seguir:
Diferença dividida de ordem 0: $\(f[x_i]=f(x_i), i=0,1,...,n\)$
Diferença dividida de ordem 1: $\(f[x_i, x_{i+1}]=\frac{f[x_{i+1}]-f[x_{i}]}{x_{i+1}-x_i}, i=0,1,...,n-1\)$
Diferença dividida de ordem 2: $\(f[x_i, x_{i+1}, x_{i+2}]=\frac{f[x_{i+1}, x_{i+2}] - f[x_{i}, x_{i+1}]} {x_{i+2} - x_i}, i=0,1,...,n-2\)$
Diferença dividida de ordem n: $\(f[x_0,...,x_n]=\frac{f[x_1,...,x_n] - f[x_0, ...,x_{n-1}]} {x_n - x_0} \)$
A seguir é apresentado um exemplo de como obter as diferenças divididas para um conjunto de 5 pontos distintos da função \(f(x)=1/x\).
Exemplo 4.2.1 : Considere os pontos \begin{array}{cccccc} \hline i &0 &1 &2 &3 &4 \ \hline x_i &1 &2 &4 &5 &8 \ f(x_i) &1.00 &0.50 &0.25 &0.20 &0.125 \ \hline \end{array}
Diferenças divididas de ordem 0:
\(f[x_0]=f(x_0)=f(1)=1.00\)
\(f[x_1]=f(x_1)=f(2)=0.50\)
\(f[x_2]=f(x_2)=f(4)=0.25\)
\(f[x_3]=f(x_3)=f(5)=0.20\)
\(f[x_4]=f(x_4)=f(8)=0.125\)
Diferenças divididas de ordem 1:
\(f[x_0,x_1]=\frac{f[x_1]-f[x_0]}{x_1-x_0}=\frac{0.5-1}{2-1}=-0.5\)
\(f[x_1,x_2]=\frac{f[x_2]-f[x_1]}{x_2-x_1}=\frac{0.25-0.5}{4-2}=-0.125\)
\(f[x_2,x_3]=\frac{f[x_3]-f[x_2]}{x_3-x_2}=\frac{0.2-0.25}{5-4}=-0.05\)
\(f[x_3,x_4]=\frac{f[x_4]-f[x_3]}{x_4-x_3}=\frac{0.125-0.2}{8-5}=-0.025\)
Diferenças divididas de ordem 2:
\(f[x_0,x_1,x_2]=\frac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}=\frac{-0.125-(-0.5)}{4-1}=0.125\)
\(f[x_1,x_2,x_3]=\frac{f[x_2,x_3]-f[x_1,x_2]}{x_3-x_1}=\frac{-0.05-(-0.125)}{5-2}=0.025\)
\(f[x_2,x_3,x_4]=\frac{f[x_3,x_4]-f[x_2,x_3]}{x_4-x_2}=\frac{-0.025-(-0.05)}{8-4}=0.00625\)
Diferenças divididas de ordem 3:
\(f[x_0,x_1,x_2,x_3]=\frac{f[x_1,x_2,x_3]-f[x_0,x_1,x_2]}{x_3-x_0}=\frac{0.025-0.125}{5-1}=-0.025\)
\(f[x_1,x_2,x_3,x_4]=\frac{f[x_2,x_3,x_4]-f[x_1,x_2,x_3]}{x_4-x_1}=\frac{0.00625-0.025}{5-2}=-0.003125\)
Diferenças divididas de ordem 4:
\(f[x_0,x_1,x_2,x_3,x_4]=\frac{f[x_1,x_2,x_3,x_4]-f[x_0,x_1,x_2,x_3]}{x_4-x_0}=\frac{-0.003125-(-0.025)}{8-1}=0.003125\)
Para facilitar o cálculo dessas diferencas divididas, é conveniente construir uma tabela em que cada coluna, a partir da terceira, é obtida usando as diferencas entre elementos consecutivos da coluna anterior e valores correspondentes da coluna de \(x_i\). Para o exemplo anterior a tebela ficaria como é mostrado a seguir:
\begin{eqnarray*} x_i& & &f[x_i]& &f[x_i,x_{i+1}]& &f[x_i,\dots,x_{i+2}]& &f[x_i,\dots,x_{i+3}]& &f[x_i,\dots,x_{i+4}]\ \hline 1& & &1& &-0.5& &0.125& &-0.025& &0.003125\ 2& & &0.5& &-0.125& &0.025& &-0.003125\ 4& & &0.25& &-0.05& &0.00625\ 5& & & 0.2& &-0.025\ 8& & &0.125 \end{eqnarray*}
Uma vez calculadas as diferenças divididas, usa-se o seguinte método recursivo para avaliar o polinômio em um determinado valor de \(x\)
\(P_0(x) = f[x_0,\dots,x_n]\)
\(P_1(x) = f[x_0,\dots,x_{n-1}]+ (x-x_{n-1})P_0(x)\)
\(P_2(x) = f[x_0,\dots,x_{n-2}]+ (x-x_{n-2})P_1(x)\)
\(\vdots\)
\(P_n(x) = f[x_0]+ (x-x_0)P_n(x)\)
Exemplo 4.2.1 Considere a função \(f(x)=e^x +sen(x)\) tabelada nos pontos \(x_0=0.0\), \(x_1=0.5\) e \(x_2=1.0\). Determine o polinômio interpolador usando a fórmula de Newton e avalie \(f(0.7)\).
Vamos fazer isso, inicialmente de um modo “não vetorizado”.
import matplotlib.pyplot as plt
import numpy as np
# Definindo a lista de pontos a serem interpolados
X = [0., 0.5, 1.0]
# Definindo a função a ser interpolada
f = lambda x: np.exp(x)+np.sin(x)
# Calculando os valores de f(xi)
Y = f(X)
print (np.around(X,4))
print (np.around(Y,4))
[0. 0.5 1. ]
[1. 2.1281 3.5598]
# Criando uma lista de listas para a tabela de diferencas divididas
dd=[Y] #ordem 0
# Gerando a tabela de dif. div. a partir da ordem 1 em diante
for o in range(1, len(X)):
dd.append([]) # Adiciona uma lista vazia para armazenar as dds de ordem 1
for k in range(0, len(X)-o, 1):
valor = (dd[o-1][k+1]-dd[o-1][k])/(X[k+o]-X[k])
dd[o].append(valor)
print (np.around(dd[o],4))
[2.2563 2.8632]
[0.6069]
def produtorio(x,n):
prod = 1.
for i in range(n):
prod = prod * (x-X[i])
return prod
def calculaP(x):
soma = dd[0][0]
for i in range(1,len(X)):
soma = soma + produtorio(x,i)*dd[i][0]
return soma
print ("P(0.7) =", calculaP(0.7))
# Cria a lista de pontos e calcula os valores para p plot
Xp = np.linspace(X[0], X[-1], num=10)
Yp = []
for x in Xp:
y = calculaP(x)
Yp.append(y)
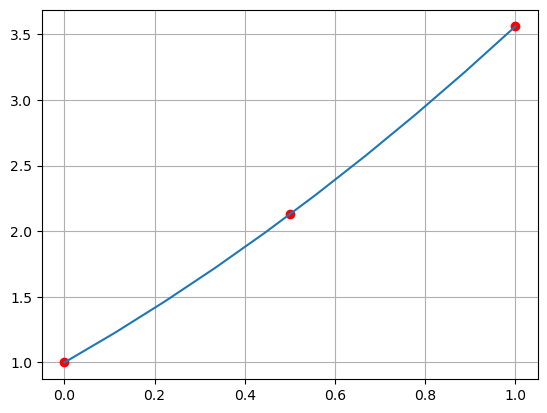
plt.plot(X, Y, 'ro', Xp, Yp,'-', )
plt.grid()
plt.show()
P(0.7) = 2.664374107530382
Melhorando (vetorizando) nosso algoritmo
Observe que as colunas da tabela de diferenças divididas mostradas no Exemplo 4.2.1 podem ser calculadas de forma bastante prática usando operações vetoriais entre numpy.arrays, por exemplo as diferencas divididas de ordem 1 podem ser obtidas fazendo (f[1:]-f[0:-1])/(x[1:]-x[0:-1]) sendo x e f arrays contendo os dados de \(x_i\) e \(f(x_i)\) conforme é mostrado a seguir:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1.,2.,4.,5.,8.])
f = 1/x
(f[1:]-f[0:-1])/(x[1:]-x[0:-1])
array([-0.5 , -0.125, -0.05 , -0.025])
fazendo um laço de repetição para as linhas seguintes podemos obter a tabela de diferenças divididas como é mostrado abaixo:
n = len(x)
for i in range(1,n+1):
print (f)
f= (f[1:]-f[0:-1])/(x[i:n]-x[0:n-i])
[1. 0.5 0.25 0.2 0.125]
[-0.5 -0.125 -0.05 -0.025]
[0.125 0.025 0.00625]
[-0.025 -0.003125]
[0.003125]
Por fim, como precisamos apenas do primeiro elemento de cada linha acima, bastaria armazenar os resultados em um único arraycomo é mostrado abaixo
f = 1/x
for i in range(1,n):
f[i:n] = (f[i:n] - f[i-1])/(x[i:n] - x[i-1])
print (f)
[ 1. -0.5 0.125 -0.025 0.003125]
Vamos agora melhorar nosso algoritmo usando a vetorização do código.
Exemplo 4.2.2:
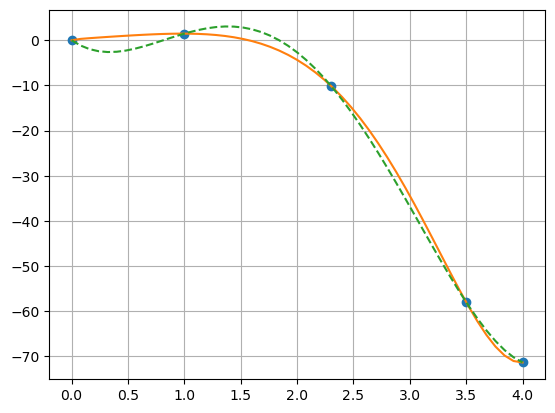
Seja a função \(f(x)=e^xcos(x)\sqrt{x}\) tabelada nos pontos \(x_0=0.0\), \(x_1=1.0\), \(x_2=2.3\), \(x_3=2.5\) e \(x_4=4.0\). Vamos usar a fórmula de interpolatória de Newton para obter o gráfico do polinômio que interpola esses pontos calculando o valor numérico do poliômio em conjunto discreto de pontos. Também vamos obter uma forma analítica para esse polinônio usando Python.
# Definindo a lista de pontos a serem interpolados
func = lambda x: np.exp(x)*np.cos(x)*np.sqrt(x)
xi = np.array([ 0, 1.0, 2.3, 3.5, 4.0])
yi = func(xi)
# uma função para calcular as diferenças divididas
def difdiv(x,y):
m = len(x)
dd = y.copy()
for k in range(1,m):
dd[k:m]=(dd[k:m]-dd[k-1])/(x[k:m]-x[k-1])
return dd
f = difdiv(xi,yi)
print(f)
[ 0. 1.46869394 -4.50049655 -2.26454299 2.25023479]
def calculaP(f,xi,x):
n = len(xi) - 1
p = f[n]
for i in range(1,n+1):
p = f[n-i] + (x -xi[n-i])*p
return p
# Cria a lista de pontos para o plot
xp = np.linspace(0, 4, num=51)
yp = []
for x in xp:
yp.append(calculaP(f,xi,x))
# Plota
plt.plot(xi, yi, 'o',
xp, func(xp),'-',
xp, yp,'--')
plt.grid()
plt.show()
Exemplo 4.2.3:
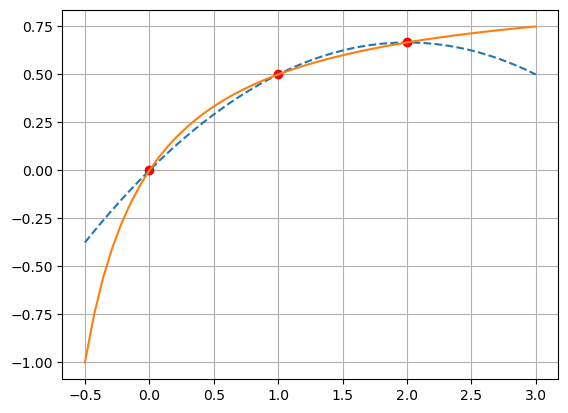
Considere a função \(f(x)=\frac{x}{(x+1)}\) tabelada nos pontos \(x_0=0.0\), \(x_1=1.0\) e \(x_2=2.0\). Determine o polinômio interpolador usando a fórmula de Newton e avalie \(f(1.3)\).
xi = np.array([0., 1.0, 2.0])
func = lambda x: np.divide(x, x + 1)
yi = func(xi)
f = difdiv(xi,yi)
print (f)
[ 0. 0.5 -0.16666667]
print ("P(1.3) =", calculaP(f,xi,1.3))
xp = np.linspace(-0.5, 3)
yp = []
for x in xp:
yp.append(calculaP(f,xi,x))
plt.plot(xi, yi, "ro",
xp, yp, "--",
xp, func(xp),"-")
plt.grid()
plt.show()
P(1.3) = 0.5850000000000001
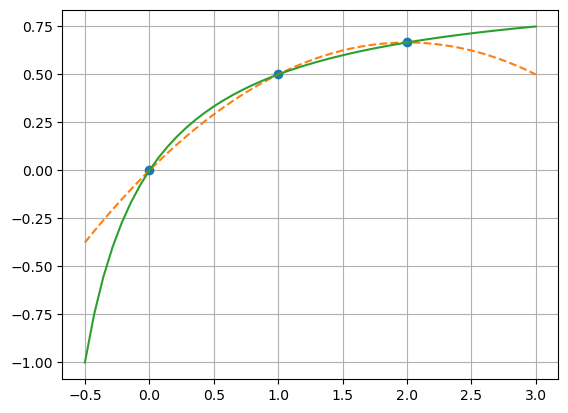
A biblioteca SciPy para computação científica em Python possui diversos algoritmos para interpolação uni e multidimensional, incluindo splines, métodos de Lagrange e baseados em série de Taylor. Veja como fica fácil com o exemplo abaixo.
from scipy.interpolate import lagrange
a = lagrange(xi, yi)
print(a.coef)
[-0.16666667 0.66666667 0. ]
plt.plot(xi, yi, 'o',
xp, np.polyval(a,xp),'--',
xp, func(xp),"-")
plt.grid()
plt.show()
Para saber mais, pesquise sobre scipy.interpolate na internet.
Interpolação Inversa#
Denominamos interpolação inversa quando, conhecidos os valores de uma função \(f(x)\) definida em \((n+1)\) pontos distintos \(x_i\) ,\(i =0,...,n\), necessitamos calcular o valor numérico da variável \(x\) correspondente a um valor \(y = f(x)\) conhecido inicialmente.
Supondo que a função inversa de \(f (x)\) exista no intervalo de interpolação, a qual denotamos por \(f^{-1}(x)\), então para os pontos tabelados \( y_i = f(x_i) \), \(i = 0,...,n\) temos \(x_i =f^{-1}(y_i)\), e o valor desejado \(x\) tal que \(y=f(x)\) é obtido por \(x=f^{-1}(y)\).
Assim, simplesmente trocamos na tabela de dados os valores de \(x\) e \(f(x)\) e fazemos a interpolação de \(f^{-1}(x)\), como visto anteriormente.
Lembramos, ainda, que a função inversa \(x = f^{-1}(y)\) existe e é única se \(f(x)\) é contínua e monótona crescente ou decrescente no intervalo de interpolação.
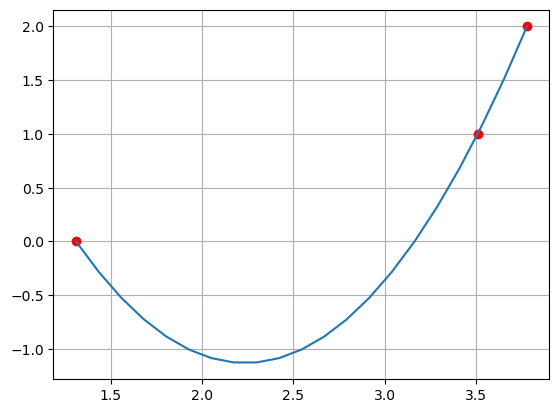
Exemplo 4.2.4:
Considere uma função \(f (x)\) tabelada, como segue:
Usando interpolação inversa, determine \(x\) tal que \(f(x) = 3.63\).
yi = np.array([0.00, 1.00, 2.00])
xi = np.array([1.31, 3.51, 3.78])
def evalPoly(dd,xi,x):
n = len(xi) - 1
# Degree of polynomial
p = dd[n]
for k in range(1,n+1):
p = dd[n-k] + (x -xi[n-k])*p
return p
def coeffts(xi,yi):
m = len(xi)
# Number of data points
dd = yi.copy()
for k in range(1,m):
dd[k:m] = (dd[k:m] - dd[k-1])/(xi[k:m] - xi[k-1])
return dd
dd = coeffts(xi,yi)
print ('dd',dd)
print("P(3.63)=",evalPoly(dd,xi,3.63))
Xplot = np.linspace(xi[0], xi[-1], 21)
Yplot = []
for x in Xplot:
Yplot.append(evalPoly(dd,xi,x))
plt.plot(xi, yi, "ro", Xplot, Yplot, "-")
plt.grid()
plt.show()
dd [0. 0.45454545 1.31544868]
P(3.63)= 1.4207663681347895
Exercícios#
1. Considere os dados, $\( \begin{array}{cccccc} \hline x &1,6 &1,9 &2,5 &3,2 &3,9 &4,5 \\ \hline f(x) &2,0 &8,0 &14,0 &15,5 &9,0 &2,1 \\ \hline \end{array} \)$
(a) Calcule \(f(2,9)\) usando polinômios interpoladores de Newton de segundo a quarto graus. Escolha a sequência de pontos que julgar mais adequada.
(b) Utilize a expressão
para fazer uma estimativa do erro em cada uma das previsões.
(c) Para o polinômio que forneceu o melhor resultado, use a fórmula de Lagrange com os mesmos pontos e compare o resultado. Comente o que você observou.
2. O volume específico de um vapor superaquecido está listado nas tabelas de vapor para diversas temperaturas. por exemplo, na pressão absoluta de 3000 lb/pol\(^2\):
Use interpolação para obter uma tabela que forneça \(v\) a cada 5\(^\circ\) entre as temperaturas 720\(^\circ\) e 760\(^\circ\) usando a fórmula de Lagrange e a fórmula de Newton. Compare os resultados e comente o que você observou.
3. Após serem efetuadas medições num gerador de corrente contínua, foram obtidos os seguintes valores indicados por um voltímetro e um amperímetro. $\( \begin{array}{ccccccccccccc} \hline I(A) &1.58& 1.75& 2.10& 2.20& 2.50& 3.50& 3.75& 4.25& 4.50& 4.90& 3.12 \\ \hline V(v) &210& 165& 154& 120& 85& 50& 73& 76& 110& 128& 60 \\ \hline \end{array} \)\( Faça um gráfico dos dados.(a) Ajuste os dados por polinômio de grau adequado. (b) Estime o valor a ser obtido no voltímetro quando o amperímetro estiver marcando \)4.0A$.
4. Considere a função $\(f(x)=\frac{3.21}{0.73 + 9.81x^2}\)$
(a) Aproxime o valor de \(f(1.78)\) usando um polinômio interpolador de grau 3 no intervalo [1, 2] e compare com o valor da função. Mostre o gráfico do polinômio e da função nesse intervalo. (b) Repita o item anterior, mas dessa vez utilize um polinômio de grau 10 no intervalo [-2,2] e comente o que você observou. (c)Pesquise e responda o que é “Fenômeno de Runge”.
5. Dada a tabela a seguir, de valores de uma função \(f\),
(a) Utilize todos os pontos para obter uma estimativa para \(f(0,22)\) usando um polinômio interpolador com a fórmula de Newton.
(b) Plote o gráfico do polinômio obtido juntamente com os pontos tabelados para verificar o resultado da interpolação.
(c) Escolha 4 pontos e estime \(f(0,22)\) utilizando um polinomio de terceiro grau. Plote o gráfico e compare com o resultado do item anterior. Comente.
