5.1 Minimos quadrados: caso discreto#
O método dos mínimos quadrados é útil quando queremos aproximar uma função \(f(x)\) por uma outra função \(g(x)\), seja porque \(f\) não tem expressão analítica conhecida, ou por ser de difícil tratamento ou manipulação. A função \(g(x)\) pode ser uma combinação de funções polinomiais, exponenciais, logarítmicas, trigonométricas, etc.
De forma geral, escrevemos a função \(g(x)\) como uma combinação linear das funções \(g_1(x)\), \(g_2(x)\),…,\(g_n(x)\), ou seja:
O problema a ser resolvido, portanto, se resume em encontrar os parâmetros \(a_1\), \(a_2\), …, \(a_n\) para função \(g(x)\) que melhor aproxima a função \(f(x)\).
No caso discreto \(f(x)\) é utilizado apenas num conjunto finito de pontos e no caso contínuo é usada a expressão analítica da função \(f(x)\).
Para encontrar a função \(g(x)\) que melhor “se ajusta” aos \(n\) pontos conhecidos de uma função \(f(x)\) devemos buscar minimizar os desvios, ou erros, \(e(x_i) = f(x_i)-g(x_i)\), \(i=1,...,m\). No método dos mínimos quadrados, se a função for conhecida apenas em um conjunto finito de pontos, fazemos isso minimizando a soma
Note que, diferentemente do que aproximar \(f\) por interpolação, com mínimos quadrados, função \(g(x)\) não necessariamente precisa passar pelos pontos mas sim se ajustar a eles.
Se \(f\) for conhecida, buscamos minimizar a função
ou seja, queremos minimizar a área entra os gráficos de \(g(x)\) e \(f(x)\).
O caso discreto é útil quando queremos aproximar uma função complicada por outra mais simples, ou então, obter uma função que possa representar um conjunto de dados obtidos experimentalmente usamos. Por exemplo, se quisermos encontrar a função linear que representa o comportamento de uma mola a partir de medidas da força \(F\) aplicada para esticar essa mola e o do comprimento \(x\) da mola esticada, podemos buscar a função linear \(F(x)=kx\) (Lei de Hooke), encontrando constante elástica \(k\) que determina a reta que melhor se ajusta aos dados.
Caso discreto#
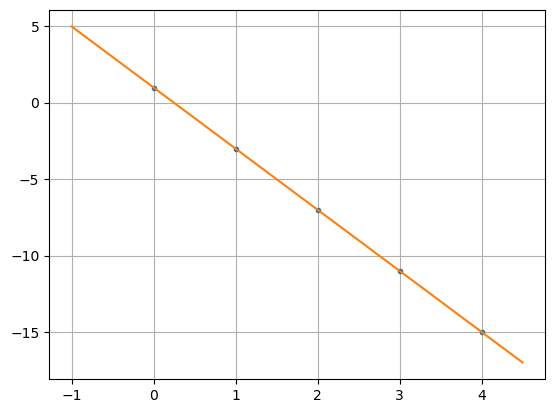
Inicialmente vamos supor que queremos ajustar uma reta \(g(x) = a_1x+a_2\) aos pontos \((x_i, f(x_i))\), \(i=1,...,m\), como é mostrado na figura abaixo
 m
m
Então, buscamos os coeficientes \(a_1\) e \(a_2\) que definem a reta que melhor se ajusta aos pontos, ou seja, os coeficientes que minimizam a função
Do cálculo infinitesimal, sabemos que se a função \( E(a_1, a_2)\) possui um ponto de mínimo, suas derivadas parciais nesse ponto devem ser nulas, ou seja
Derivando \( E(a_1, a_2)\) em relação a \(a_1\) e \(a_2\) obtemos
ou
ou, ainda
e
As equações obtidas nos permitem encontrar \(a_1\) e \(a_2\) por meio da resolução do sistema linear
ou
Exemplo 1: Ajuste uma reta à função \(f(x)\), tabelada como segue
Resolução: Fazendo
\(\sum_{i=1}^{5} x_i^2 = 0^2+1^2+2^2+3^2+4^2 = 30\)
\(\sum_{i=1}^{5} x_i = 0+1+2+3+4 = 10\)
\(\sum_{i=1}^{5} f(x_i)x_i = 0\times0.98+1\times(-3.01)+2\times(-6.99) +3\times(-11.01)+4\times(-15) = -3.996\)
\(\sum_{i=1}^{5} x_i = 0.98+(-3.01)+(-6.99) +3\times(-11.01)+(-15) = -3.996\)
Então, fazendo
Obtem-se
cuja solução fornece
Que são os coefinientes da reta procurada ]
import numpy as np
from scipy.linalg import solve
import matplotlib.pyplot as plt
X = np.array([0, 1, 2, 3, 4])
Y = np.array([0.98, -3.01, -6.99, -11.01, -15.0])
# Calcula os elementos das marizes
a11 = np.sum(X**2)
a12 = np.sum(X)
a22 = len(X)
b1 = np.sum(X * Y)
b2 = np.sum(Y)
# Monta e resolve o sistema
A = np.array([[a11, a12], [a12, a22]])
print (A)
B = np.array([b1,b2])
print (B)
a = solve(A, B)
print (a)
# define a funcao g(x) para plotar
g = lambda x: a[0]*x+a[1]
# cria pontos (x, y) da reta
Xr = np.arange(-1, 5, 0.5)
# Plota os pontos e a reta
plt.plot(X, Y, ".", Xr, g(Xr), "-")
plt.grid()
plt.show()
[[30 10]
[10 5]]
[-110.02 -35.03]
[-3.996 0.986]
Para aproximar a função f(x) por um polinômio de grau 2, usamos a seguinte forma geral para \(g(x)\)
com \(g_1(x) = x^2\), \(g_2(x) = x\) e \(g_3(x) = 1\).
Procuramos o ponto de mínimo, em que as derivadas parciais são nulas, ou seja
Derivando \( E(a_1, a_2, a_3)\) em relação a \(a_1\), \(a_2\) e \(a_3\) obtemos
ou
ou, ainda
analogamente, derivando em relação a \(a_2\)
e em relação a \(a_3\)
Assim, as equações obtidas nos permitem montar um sistema linear cuja solução dará os coeficientes \(a_1\), \(a_2\) e \(a_3\) procurados
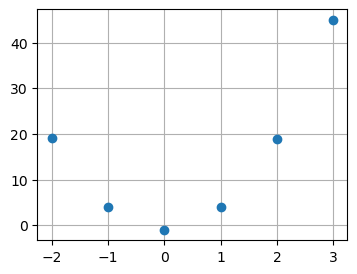
Exemplo 2: Considere uma função f (x) definida conforme tabela
Observando o gráfico, vemos que a função possui o comportamento de uma parábola, ou seja, podemos ajustar um polinômio de grau 2.
X = np.array([-2., -1., 0, 1., 2., 3.])
Y = np.array([19.01, 3.99, -1.00, 4.01, 18.99, 45.00])
plt.figure(figsize=(4,3))
plt.plot(X, Y, "o")
plt.grid()
plt.show()
Assim, tomamos \(g(x)=a_1 x^2+a_2 x+a_3\), isto é, \(g_1(x)=x^2, g_2(x)=x, g_3(x)=1\), e determinamos os parâmetros \(a_1, a_2\) e \(a_3\) de modo que \(g(x)\) se ajuste aos dados. Substituindo no sistema de equações normais temos:
ou
Vamos fazer essas contas em Python:
# Monta o sistema
A = np.array([[np.sum(X**4), np.sum(X**3), np.sum(X**2)],
[np.sum(X**3), np.sum(X**2), np.sum(X) ],
[np.sum(X**2), np.sum(X), len(X)] ])
B = np.array([np.sum(X**2*Y),
np.sum(X*Y) ,
np.sum(Y) ])
print(A)
print(B)
[[115. 27. 19.]
[ 27. 19. 3.]
[ 19. 3. 6.]]
[565. 134.98 90. ]
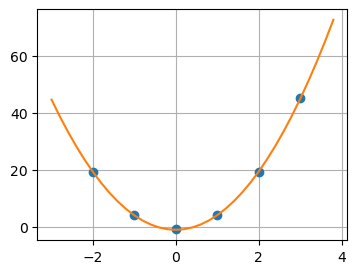
A solução do sistema nos fornece \( a_1=5,0898\), \(a_2=0,0519\) e \(a_3=-1,1437\) como podemos ver a seguir. Ou seja, a função que procuramos é \(g(x) = 5,0898x^2 + 5,0898x -1,1437 \). Vamos plotar essa função junto com os pontos:
a = solve(A, B)
print (a)
[ 5.08982143 0.05189286 -1.14371429]
# define a funcao g(x) para plotar
g = lambda x: a[0]*x*x+a[1]*x+a[2]
# gera os pontos
Xr = np.arange(X[0]-1, X[-1]+1, 0.2)
Yr = []
for x in Xr:
Yr.append(g(x))
# plota
plt.figure(figsize=(4,3))
plt.plot(X, Y, "o", Xr, Yr, "-")
plt.grid()
plt.show()
Forma matricial do sistema#
Observe que podemos obter o mesmo resultado se fizermos \(A= V^TV\) e \(B=V^T y_i\), onde \(V\) é a matriz cujas linhas são formadas por \([g_1(x_i) \,\, g_n(x_i) \,\,... \,\,g_n(x_i)\,\,]\), \(i=1,...,m\). Nesse caso, a solução pode ser obtida fazendo:
Observe os códigos a seguir:
V = np.array([X**2, X**1, X**0]).T
print (V)
[[ 4. -2. 1.]
[ 1. -1. 1.]
[ 0. 0. 1.]
[ 1. 1. 1.]
[ 4. 2. 1.]
[ 9. 3. 1.]]
A = np.dot(V.T,V)
print (A)
[[115. 27. 19.]
[ 27. 19. 3.]
[ 19. 3. 6.]]
B = np.dot(V.T,Y)
print('B=',B)
B= [565. 134.98 90. ]
a = np.linalg.solve(A,B)
print('solução:', a)
solução: [ 5.08982143 0.05189286 -1.14371429]
Ou ainda, de forma mais compacta,fazendo \( a = (V^TV)^{-1}V^Ty \):
# importando as funções para multiplicar e inverter
from numpy.linalg import inv
from numpy import dot
# resolvendo o sistema
a = inv(dot(V.T,V)).dot(dot(V.T,Y))
print('solução:', a)
solução: [ 5.08982143 0.05189286 -1.14371429]
Exercícios:#
1. Em um experimento foram obtidos os seguintes dados:
a) Determine a reta que melhor se ajusta aos dados da tabela, usando o método dos mínimos quadrados
b) Calcule a soma do erro quadrático \(\sum_{i=1}^5 (f(x_i)-g(x_i))^2\)
2. Após serem efetuadas medições num gerador de corrente contínua, foram obtidos os seguintes valores indicados por um voltímetro e um amperímetro. $\( \begin{array}{ccccccccccccc} \hline I(A) &1.58&1.75&2.10&2.20&2.50&3.50&3.75&4.25&4.8&4.9&3.12 \\ \hline V(v) &210&155&170&120&85&50&110&79&150&120&60 \\ \hline \end{array} \)\( Faça um gráfico dos dados.(a) Ajuste os dados por polinômio de grau adequado. (b) Estime o valor a ser obtido no voltímetro quando o amperímetro estiver marcando \)4.0A$.
3. Dados os seguintes pontos tabelados $\( \begin{array}{cccccccccc} \hline x_i &0.01 &0.99 &2.02 &3.01 &3.97 &5.01 &5.93 &6.99 &8.08 \\ \hline f(x_i) &0.000 &1.621 &1.782 &0.915 &-0.122 &-0.225 &1.099 &2.728 &3.534\\ \hline \end{array} \)$
Encontre o polinômio de grau 3 que melhor se ajusta aos pontos dados.
Exemplo#
p190
import numpy as np
from scipy.linalg import solve
import matplotlib.pyplot as plt
from scipy.integrate import quad
import math
from numpy import exp
g1g1 = lambda x: 1
g1g2 = lambda x: x
g2g2 = lambda x: x**2
fg1 = lambda x: -math.exp(-0.75*x)
fg2 = lambda x: -x*math.exp(-0.75*x)
# Calcula os elementos das marizes
a11 = quad(g1g1, 1, 3)[0]
a12 = quad(g1g2, 1, 3)[0]
a22 = quad(g2g2, 1, 3)[0]
b1 = quad(fg1, 1, 3)[0]
b2 = quad(fg2, 1, 3)[0]
# Monta e resolve o sistema
A = np.array([[a11, a12], [a12, a22]])
B = np.array([b1,b2])
a = solve(A, B)
print (a)
# define a funcao g(x) para plotar
g = lambda x: a[0]+a[1]*x
# cria pontos (x, y) da reta
Xr = np.arange(1, 3, 0.2)
#print (Xr)
#Y = np.exp(X)
# Plota os pontos e a reta
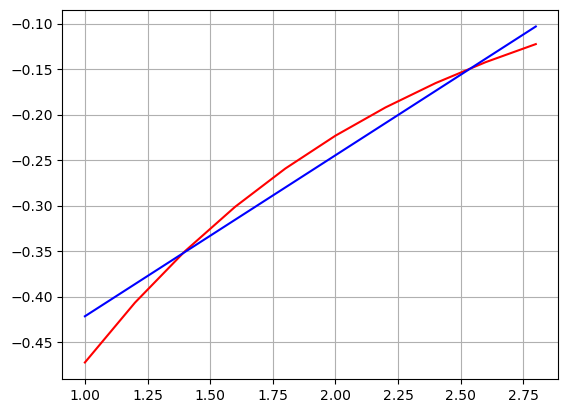
plt.plot(Xr, -np.exp(-0.75*Xr), "r-", Xr, g(Xr), "b-")
plt.grid()
plt.show()
[-0.59854891 0.17695201]
Exercícios#
1. Encontre o polinômio \(p(x) = a_1 + a_2x + a_3x^2\) que melhor se ajusta no sentido de mínimos quadrados aos pontos:
Resposta: \(a_1 = -0,67112\), \(a_2 = -0,12123\), \(a_3 = 0,73907\).
2. Encontrar a parábola \(y=ax^2+bx+c\) que melhor aproxima o seguinte conjunto de dados: $\( \begin{array}{l|ccccc} \hline i & 1 & 2 & 3 & 4 & 5 \\\hline x_i & 0,01 & 1,02 & 2,04 & 2,95 & 3,55\\ y_i & 1,99 & 4,55 & 7,20 & 9,51 & 10,82\\ \hline \end{array} \)\( _Resposta:_ \)y=-0,0407898x^2+ 2,6613293x+ 1,9364598$
3. Dado o seguinte conjunto de dados $\( \begin{array}{l|ccccccccccc} \hline x_i & 0,0 & 0,1 & 0,2 & 0,3 & 0,4 & 0,5 & 0,6 & 0,7 & 0,8 & 0,9 & 1,0\\\hline y_i & 31 & 35 & 37 & 33 & 28 & 20 & 16 & 15 & 18 & 23 & 31\\ \hline \end{array} \)$
a) Encontre a função do tipo \(f(x)=a+b\sin(2\pi x)+c\cos(2\pi x)\) que melhor aproxima os valores dados.
b) Encontre a função do tipo \(f(x)=a+bx+cx^2+dx^3\) que melhor aproxima os valores dados.
Resposta: a) \(a=25,638625\), \(b=9,8591874\), \(c=4,9751219\); b)\(a=31,475524\), \(b=65,691531\), \(c=-272,84382\), \(d=208,23621\).
Fonte: https://www.ufrgs.br/reamat/CalculoNumerico/livro-py/adc-ajuste_linear_geral.html
