5.2 Ajuste linear nos parâmetros

Uma função do tipo

\[ g(x) = a_1 g_1(x) + a_2 g_2(x) + ... + a_n g_n(x)\]

é dita um modelo de regressão linear. O adjetivo “linear” é usado para indicar que o modelo é linear nos parâmetros \(a_1\), \(a_2\),…, \(a_n\) e não porque é um função linear de \(x\). Por exemplo, uma expressão da forma

\[ y = a_1 + a_2 log(x) + a_3 x^3 \]

é um modelo de regressão linear múltipla, assim como os ajustes polinomiais feitos nos capítulos anteriores, mas o mesmo não acontece com a equação

\[y =a_1 + a_2 x^{a_3} + a_4 x^2\]

Algumas maneiras de justar funções não lineares serão discutidos nas próximas seções. Por hora, apresentamos um exemplo de ajuste linear não polinomial.

Generalizando

Generalizando o procedimento, podemos determinar os coeficientes \(a_1,a_2,...,a_n\) da função\( g(x) = a_1g_1(x)+a_1g_1(x)+...+a_ng_n(x)\) resolvendo o sistema linear formado pelas equações

\[ \frac{\partial E}{\partial a_1} = 0, \,\, \frac{\partial E}{\partial a_2} = 0, ..., \,\, \frac{\partial E}{\partial a_n} = 0\]

ou seja,

\[\begin{split} \begin{cases} \left(\sum_{i=1}^{m} g_1(x_i)g_1(x_i)\right)a_1 + \left(\sum_{i=1}^{m} g_1(x_i)g_2(x_i)\right)a_2+...+\left(\sum_{i=1}^{m} g_1(x_i)g_n(x_i)\right)a_n = \sum_{i=1}^{m} f(x_i)g_1(x_i) \\ \left(\sum_{i=1}^{m} g_2(x_i)g_1(x_i)\right)a_1 + \left(\sum_{i=1}^{m} g_2(x_i)g_2(x_i)\right)a_2+...+\left(\sum_{i=1}^{m} g_2(x_i)g_n(x_i)\right)a_n = \sum_{i=1}^{m} f(x_i)g_2(x_i) \\ \vdots\\ \left(\sum_{i=1}^{m} g_n(x_i)g_1(x_i)\right)a_1 + \left(\sum_{i=1}^{m} g_n(x_i)g_2(x_i)\right)a_2+...+\left(\sum_{i=1}^{m} g_n(x_i)g_n(x_i)\right)a_n = \sum_{i=1}^{m} f(x_i)g_n(x_i) \\ \end{cases} \end{split}\]

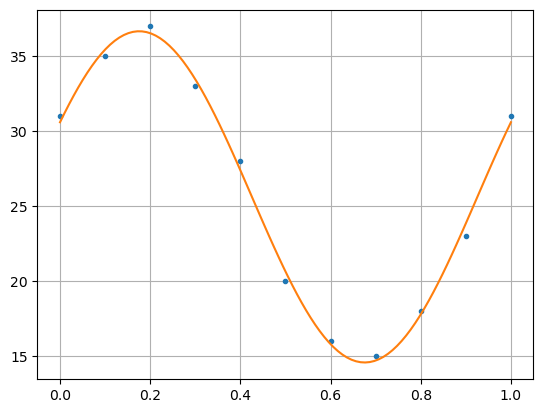
Exemplo 1: Dado o seguinte conjunto de dados $\( \begin{array}{l|ccccccccccc} \hline x_i & 0,0 & 0,1 & 0,2 & 0,3 & 0,4 & 0,5 & 0,6 & 0,7 & 0,8 & 0,9 & 1,0\\\hline y_i & 31 & 35 & 37 & 33 & 28 & 20 & 16 & 15 & 18 & 23 & 31\\ \hline \end{array} \)$

Encontre a função do tipo \(f(x)=a+b\sin(2\pi x)+c\cos(2\pi x)\) que melhor aproxima os valores dados.

import numpy as np
from scipy.linalg import solve
import matplotlib.pyplot as plt

x = np.linspace(0.0,1.0, 11)
y = np.array([31.,35.,37,33.,28.,20.,16.,15.,18.,23.,31.])

g1 = lambda x: np.ones(len(x))
g2 = lambda x: np.sin(2*np.pi*x)
g3 = lambda x: np.cos(2*np.pi*x)

V = np.array([g1(x), g2(x), g3(x)])

A = V.dot(V.T)
B = np.dot(V,y)
a = np.linalg.solve(A,B)

g = lambda x: a[0]*g1(x)+a[1]*g2(x)+a[2]*g3(x)

# Plota os pontos e a função g(x)
xp = np.linspace(0.0,1.0,100)
plt.plot(x, y, ".")
plt.plot(xp, g(xp), "-") 
plt.grid()
plt.show()

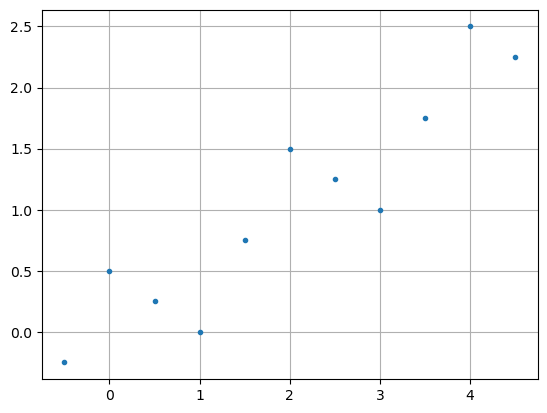
Exemplo 2: Considere o segunte conjunto de pontos

\[\begin{split}\begin{array}{cccccccccccc} x_i &-0.5 &0.0 &0.5 &1.0 &1.5 &2.0 &2.5 &3.0 &3.5 &4.0 &4.5\\ f(x_i) &-0.25 &0.5 &0.25 &0.0 &0.75 &1.5 &1.25 &1.00 &1.75 &2.5 &2.25 \end{array} \end{split}\]

Usando o método dos mínimos quadrados, ajuste uma função \(g(x)\) aos dados.

Solução: Primeiramente, construimos o diagrama de dispersão dos pontos dados:

import numpy as np
import matplotlib.pyplot as plt

X = np.array([-0.5, 0.0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5])
Y = np.array([-0.25, 0.5, 0.25, 0.0, 0.75, 1.5, 1.25, 1.00, 1.75, 2.5, 2.25])

# Plota os pontos e a reta
plt.plot(X, Y, ".") 
plt.grid()
plt.show()

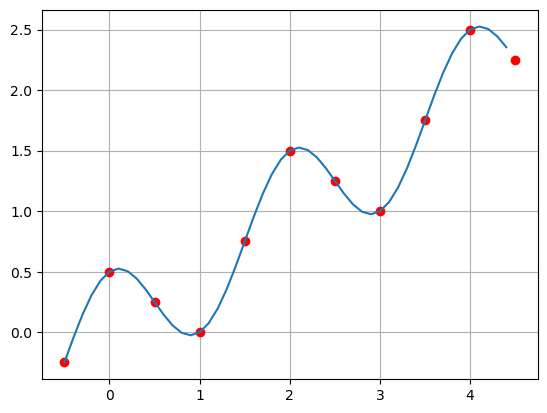
É possível perceber que os pontos parecem crescer linearmente mas também parecem oscilar com período igual a 2.

Essas características sugerem uma função do tipo \(g(x) = a_1x+a_2 \cos(\pi x)\) em que \(g_1(x)=x\) e \(g_2(x) = cos(\pi x)\).

from scipy.linalg import solve

# Calcula os elementos das marizes
g1 = lambda X: X
g2 = lambda X: np.cos(np.pi*X)

print (g1(X))
a11 = np.sum(np.multiply(g1(X),g1(X)))
a12 = np.sum(np.multiply(g1(X),g2(X)))
a21 = a12
a22 = np.sum(np.multiply(g2(X),g2(X)))

print (a11, a12, a22)

b1 = np.sum(np.multiply(Y,g1(X)))
b2 = np.sum(np.multiply(Y,g2(X)))

print (b1,b2)


# Monta e resolve o sistema
A = np.array([[a11, a12],
              [a21, a22]])

B = np.array([b1,b2])

a = solve(A, B)
print (a)

# define a funcao g(x) para plotar 
g = lambda X: a[0]*g1(X)+a[1]*g2(X)

# cria pontos (x, y) da reta 
Xr = np.arange(X[0], X[-1], 0.1)
Yr = g(Xr)   

# Plota os pontos e a reta
plt.plot(X, Y, "ro", Xr, Yr, "-") 
plt.grid()
plt.show()

[-0.5  0.   0.5  1.   1.5  2.   2.5  3.   3.5  4.   4.5]
71.5 2.0000000000000018 5.0
36.75 3.5000000000000004
[0.5 0.5]

Exercício 1: Dados os seguintes pontos tabelados $\( \begin{array}{cccccccccc} \hline x_i &0.01 &0.99 &2.02 &3.01 &3.97 &5.01 &5.93 &6.99 &8.08 \\ \hline f(x_i) &0.000 &1.621 &1.782 &0.915 &-0.122 &-0.225 &1.099 &2.728 &3.534\\ \hline \end{array} \)$

Encontre a função do tipo \(g(x)=a_1x + a_2 sen(x)\) que melhor se ajusta.

Caso contínuo

No caso da função \(f(x)\) ser conhecida, podemos ajustar a função \(g(x)\) de modo a minimizar

\[ E = \int_a^b [e(x)]^2 dx = \int_a^b [f(x)-g(x)]^2 dx\]

o que leva a necessidade de resolução do sistema linear

\[\begin{split}\left[\begin{array}{cccc} \langle g_1,g_1 \rangle &\langle g_1,g_2 \rangle &... &\langle g_1,g_n \rangle\\ \langle g_2,g_1 \rangle &\langle g_2,g_2 \rangle &... &\langle g_2,g_n \rangle\\ \vdots \\ \langle g_n,g_1 \rangle &\langle g_n,g_2 \rangle &... &\langle g_n,g_n \rangle\\ \end{array} \right] \left[\begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right] = \left[\begin{array}{c} \langle f,g_1 \rangle \\ \langle f,g_2 \rangle \\ \vdots \\ \langle f,g_n \rangle \\ \end{array} \right] \end{split}\]

Com \(\langle f,g \rangle\) sendo o produto escalar entre as funções \(f\) e \(g\), definido como

\[ \langle f,g \rangle = \int_a^b f(x)g(x)dx\]

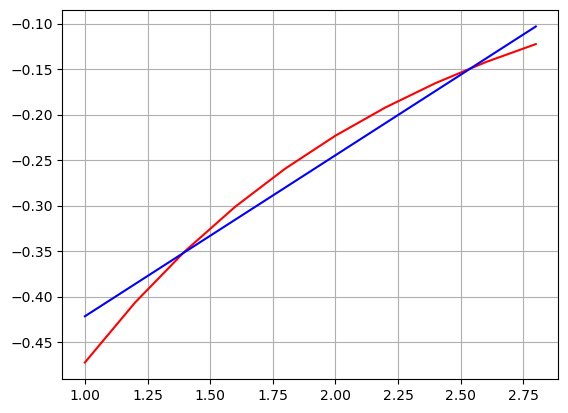
Exemplo 3: (Darezzo, 2016, p190)

import numpy as np
from scipy.linalg import solve
import matplotlib.pyplot as plt
from scipy.integrate import quad
import math
from numpy import exp

g1g1 = lambda x: 1
g1g2 = lambda x: x
g2g2 = lambda x: x**2
fg1 = lambda x: -math.exp(-0.75*x)
fg2 = lambda x: -x*math.exp(-0.75*x)




# Calcula os elementos das marizes
a11 = quad(g1g1, 1, 3)[0]
a12 = quad(g1g2, 1, 3)[0]
a22 = quad(g2g2, 1, 3)[0]
b1 = quad(fg1, 1, 3)[0]
b2 = quad(fg2, 1, 3)[0]



# Monta e resolve o sistema
A = np.array([[a11, a12], [a12, a22]])

B = np.array([b1,b2])

a = solve(A, B)
print (a)

# define a funcao g(x) para plotar 
g = lambda x: a[0]+a[1]*x

# cria pontos (x, y) da reta 
Xr = np.arange(1, 3, 0.2)
#print (Xr)

#Y = np.exp(X)

# Plota os pontos e a reta
plt.plot(Xr, -np.exp(-0.75*Xr), "r-", Xr, g(Xr), "b-") 
plt.grid()
plt.show()

[-0.59854891  0.17695201]