6.1 Integração Numérica#
A integração numérica é útil em situações nas quais não se conhece a expressão analítica da função a ser integrada ou quando a função primitiva é difícil de se obter. Uma forma de se calcular uma aproximação numérica para uma integral é por meio da integração do polinômio interpolador. Esse processo é conhecido como quadratura de Newton-Cotes e é desenvolvido por meio das sistemáticas conhecidas como Regra dos Trapézios, Regra 1/3 de Simpson e Regra 3/8 de Simpson. Antes de apresentarmos as fórmulas de Newton-Cotes, vamos relembrar um pouco do Cálculo.
Considere uma função \(f(x)\) contínua no intervalo \([a,b]\). Então, sabemos que
em que a função \(F(x)\) é a primitiva (ou antiderivada) de \(f\), ou seja, é tal que \(F'(x) = f(x)\).
Graficamente, considerando a função \(f(x) \geq 0\), para todo \(x \in [a,b]\) podemos interpretar a intergral \(I=\int_a^b f(x)dx\) como a área entre a curva de \(f\) e o eixo das abcissas:
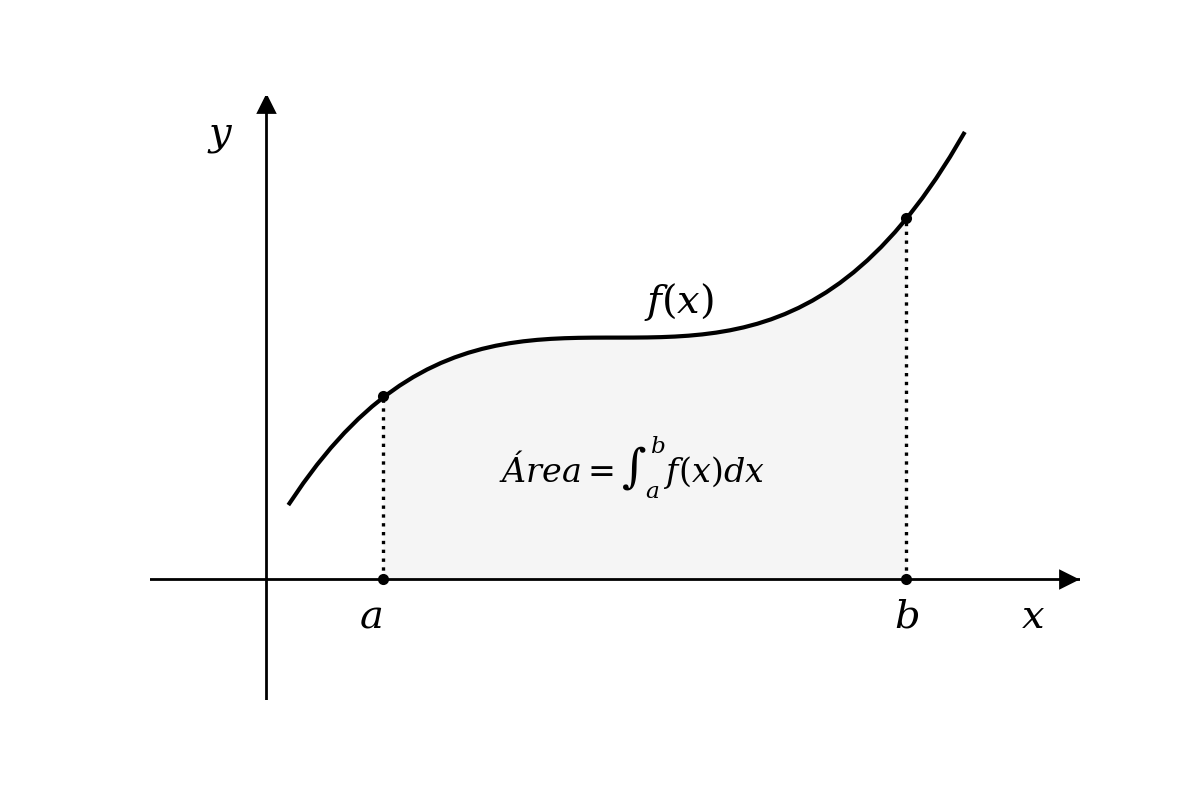
Figura 6.1 - A integral definida como área sob o gráfico
Soma de Riemann
A forma mais simples de obter um valor aproximado para uma integral definida é por meio da soma de Riemann. Para isto, divide-se o intervalo de integração \((a,b)\) em \(n\) subintervalos e somam-se as áreas dos retângulos definidos em cada subintervalo. A largura de cada retângulo será dado por \(h=\frac{x_n-x_0}{n}\) e a altura será dada por \(f(x)\) para algum \(x\) dentro do subintervalo \([x_i,x_{i+1}]\), com \(i=0,1,...,n\). Uma escolha natural para o valor de \(x\) é um dos extremos do intervalo, o extremo esquerdo \(x_i\) (“pela esquerda”) ou o extremo direito \(x_{i+1}\) (“pela direita”):

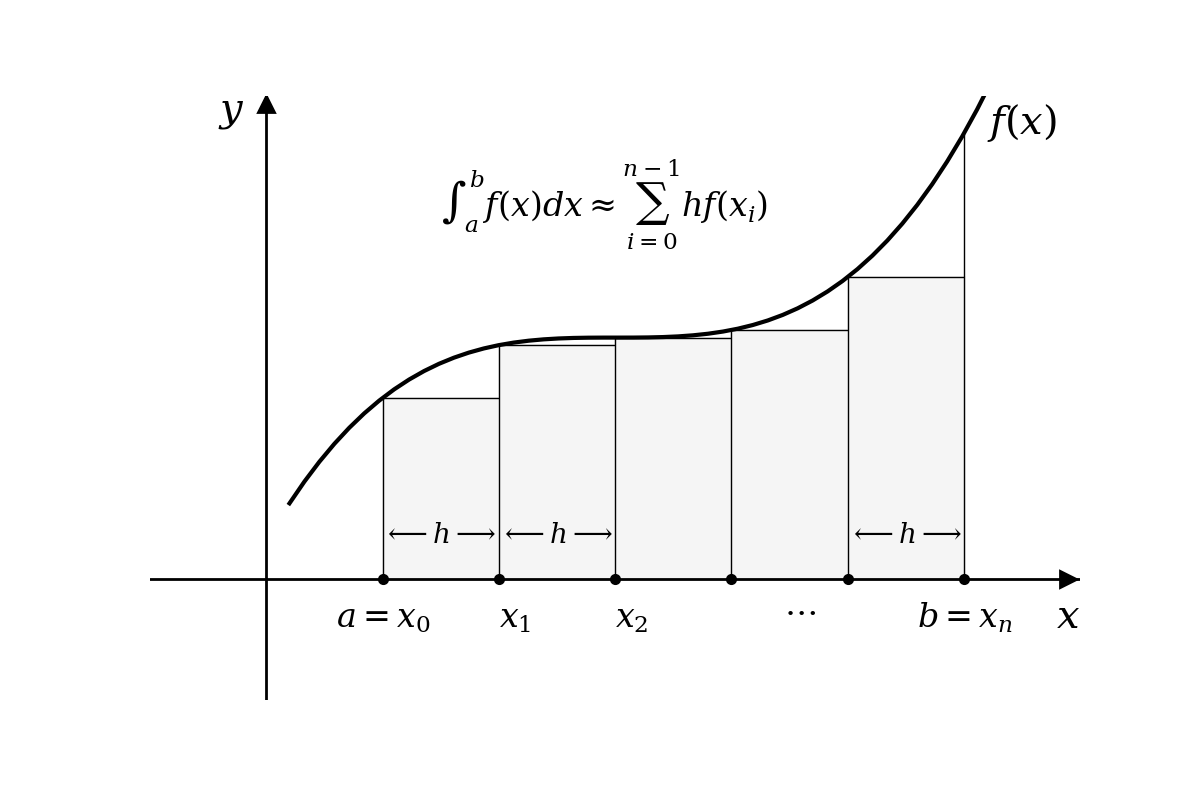
Figura 6.2 - Somas de Riemann “pela direita” e “pela esquerda”
Claramente podemos aumentar a acurácia da aproximação obtida aumentando o número de subintervalos. A regra do ponto médio considera a altura do retângulo definida em cada subintervalo como sendo o valor da função no ponto médio entre \(x_i\) e \(x_{i+1}\):
Exemplo 6.1: Nesse exemplo vamos calcular a integral \(\int_{0.1}^{0.8} x^2ln(x)dx\) usando aproximações da soma de Riemann pela esquerda, pela direita e pela regra do ponto médio, e comparar os resultados. Então vamos comparar com a solução exata (\(\approx -0.0940934155044049\)).
from math import log
F = lambda x: x**3*log(x)/3 - x**3/9
I = F(0.8)-F(0.1)
print(I)
-0.0940934155044049
Aproximado pela soma de Riemann com 7 subintervalos, ou seja, \(h = 0.1\)
import numpy as np
xi = np.linspace(0.1, 0.8, 8)
h = xi[1]-xi[0]
print ("h=",h)
h= 0.1
f = lambda x: x**2*np.log(x)
Ie = h*np.sum(f(xi[0:-1]))
print("Ie=",Ie, "Erro=",abs(I-Ie))
Ie= -0.08743221791422254 Erro= 0.006661197590182369
Id = h*np.sum(f(xi[1:]))
print("Id=",Id, "Erro=",abs(I-Id))
Id= -0.09941082010533792 Erro= 0.0053174046009330095
Im = h*np.sum(f((xi[0:-1]+xi[1:])/2))
print("Im=",Im, "Erro=",abs(I-Im))
Im= -0.09443022564968762 Erro= 0.00033681014528270936
Nesse exemplo é possivel notar que a regra do ponto médio forneceu a melhor aproximação.
De modo geral, os métodos numéricos para cálculo de integrais definidas consistem em aproximar a função \(f(x)\) pelo polinômio interpolador \(P(x)\) e integrar o polinômio. Os casos ilustrados acima são polinômios de grau zero, mas poderiamos utilizar polinômios de grau maior.
Assim, de forma geral temos:
A seguir serão apresentados três métodos para integração numérica baseados na integração do polinômio interpolador conhecidos como Regras de Newton-Cotes. São eles, a regra dos trapézios, a regra 1/3 de Simpson e a regra 3/8 de Simpson.
