6.4 Regras de Simpson

Regra 1/3 de Simpson

Consiste em aproximar a integral da função pela integral de um polinômio interpolador de grau 2. Para isso dividimos o intervalo de integração subintervalos e a cada 3 pontos usamos a integral do polinômio interplolador como aproximação da integral da função nesses dois subintervalos.

Então, considere uma função \(f(x)\) definida em três pontos distintos \(x_0\), \(x_1\) e \(x_2\) equidistantes no intervalo \([a,b]\). O polinômio de Lagrange para esses pontos, considerando a mudança de variável \(u = \frac{x-x_0}{h}\) é dado por

\[ P_2(u) = f(x_0) \left( \frac{u^2-3u+2}{2}\right) + f(x_1)\left( \frac{u^2-2u}{-1}\right) + f(x_2)\left( \frac{u^2-u}{2}\right)\]

A integral pode ser aproximada como segue

\[ \int_{x_0}^{x_n} f(x) dx \approx \int_{x_0}^{x_2} P_2(x) dx= h \int_{0}^{2} P_2(u) du \]

ou, ainda,

\[ h \int_{0}^{2} P_2(u) du = h f(x_0)(u) \Big|_0^2 + h (f(x_1)-f(x_0))\left( \frac{u^2}{2} \right) \Big|_0^2 + \frac{h}{2}(f(x_ 2)-2f(x_1)+f(x_ 0)) \left(\frac{u^3}{3}-\frac{u^2}{2} \right) \Big|_0^2 =\]

\[ = 2hf(x_0)+2hf(x_1)-2hf(x_0)+\frac{h}{3} ( f(x_2)-2f(x_1)+f(x_0)) = \]

\[ \frac{h}{3}[f(x_0)+4f(x_1)+f(x_2)]\]

Assim, temos

\[ \int_{x_0}^{x_n} f(x) dx \approx \frac{h}{3}[f(x_0)+4f(x_1)+f(x_2)]\]

conhecida como Regra 1/3 de Simpson.

Graficamente, tem-se

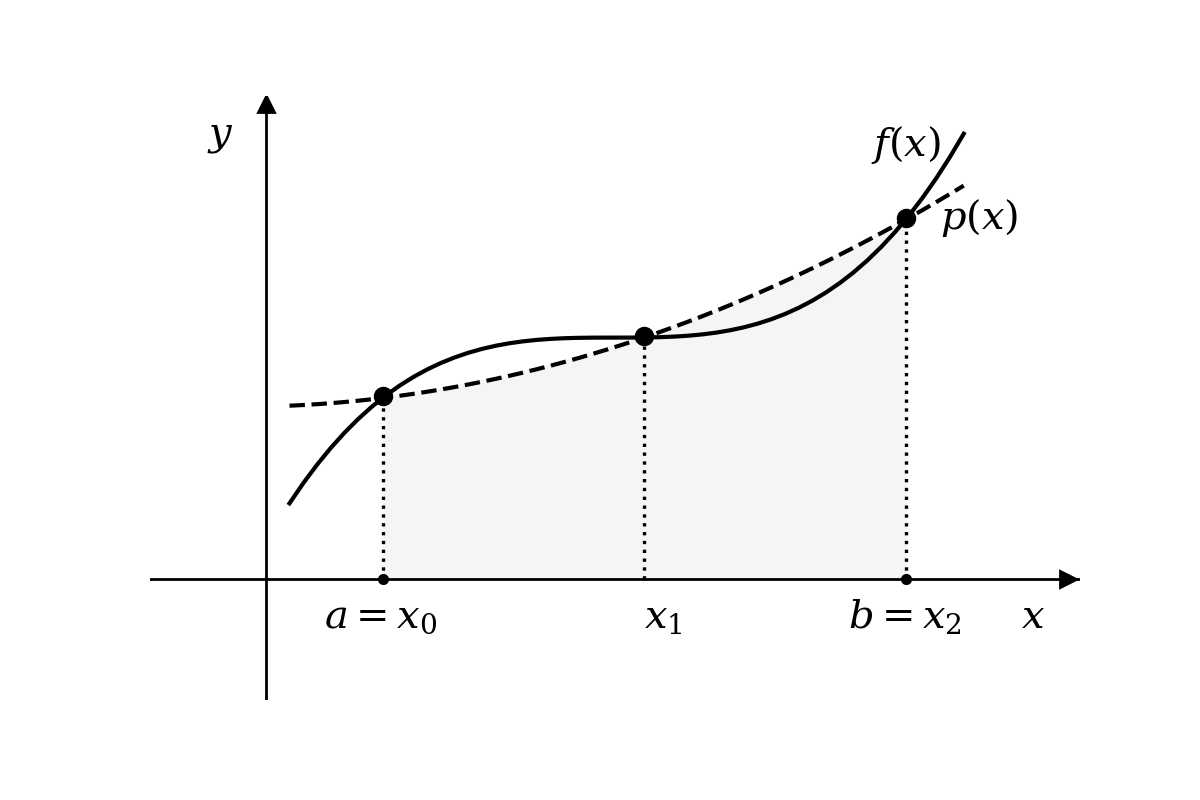
Figura 6.4 - Aproximação pela integral do polinômio interpolador de grau 2

Um limitante superior para o erro será dado por

\[ |E_2| \leq \frac{h^5}{90} max.\{|f^{(4)}(x)|, x_0 \leq \xi \leq x_2 \}\]

Exemplo 1: Calcule o valor aproximado da integral \(\int_{0.5}^{1.5}cos(x)dx\) usando a regra 1/3 de Simpson.

import numpy as np

x0 = 0.5; xn = 1.5 
n = 2
h = (xn-x0)/n

f = lambda x: np.cos(x)
xi = np.linspace(x0, xn, n+1)
yi = f(xi)

# Regra 1/3 de Simpson 
Is = (h/3)*(yi[0] + 4*yi[1] + yi[2])
print ("Resultado 1/3 Simpson: ", Is)

Resultado 1/3 Simpson:  0.5182548311717724

A biblioteca scipy contém diversas funções para integração numérica, dentre elas as regras de Simpson. Veja um exemplo de como utilizar a seguir:

import scipy.integrate as integrate
integrate.simpson(yi, x=xi)

0.5182548311717724

A regra 1/3 de Simpson repetida (ou generalizada) consiste em subdividirmos o intervalo de integração \([a,b]\) em \(n\) subintervalos de ampliture \(h\), que que \(n\) é um número par de subintervalos, com \(x_0=a\) e \(x_n=b\), então, aplicando a regra 1/3 de Simpson a cada 2 subintervalos consecutivos, obtemos

\[ \int_{x_0}^{x_n} f(x) dx \approx \frac{h}{3} [f(x_0)+4f(x_1)+f(x_2)] + \frac{h}{3} [f(x_2)+4f(x_3)+f(x_4)] + ... + \frac{h}{3} [f(x_{n-2})+4f(x_{n-1})+f(x_n)]=\]

\[ = \frac{h}{3} [f(x_0)+ 4f(x_1) + 2f(x_2)+ 4f(x_3)+...+2f(x_{n-2})+4f(x_{n-1})+f(x_n)] = \]

\[ = \frac{h}{3} \{f(x_0)+ 4[f(x_1) + f(x_3)+...+f(x_{n-1})]+ 2[f(x_2) + f(x_4)+...+f(x_{n-2})] + f(x_n)\} \]

Um limitante superior para o erro será dado por

\[ |E_2| \leq \frac{h^4}{180}(x_n-x_0) \,\, max.\left\{\left|f^{(4)}(x)\right|, x_0 \leq \xi \leq x_n \right\}\]

Exemplo 6.4: Calcule o valor aproximado da integral \(\int_1^4(xe^x+3)dx\) usando a regra 1/3 de Simpson para 10, 20 e 100 subintervalos

x0 = 1.0; xn = 4.0 
f = lambda x: x*np.exp(x)+3

for n in [10,20,100]:
    h = (xn-x0)/n
    x = np.linspace(x0, xn, n+1) 
    y = f(x)
    I = (h/3)*(y[0] + 4*np.sum(y[1:n:2]) + 2*np.sum(y[2:n:2])+ y[-1])
    print ("n=",n,", I=",I)

n= 10 , I= 172.8109327815904
n= 20 , I= 172.79549085115607
n= 100 , I= 172.79445177011632

xi = np.linspace(1, 4, 11)
print(integrate.simpson(f(xi), x=xi))

172.81093278159045

xi = np.linspace(1, 4, 21) 
print(integrate.simpson(f(xi), x=xi))

172.79549085115613

xi = np.linspace(1, 4, 101) 
print(integrate.simpson(f(xi), x=xi))

172.79445177011632

Regra 3/8 de Simpson

Consiste em aproximar a integral da função pela integral de um polinômio interpolador de grau 3. Para isso dividimos o intervalo de integração subintervalos e a cada 4 pontos usamos a integral do polinômio interpolador como aproximação da integral da função nesses 3 subintervalos.

Então, considere uma função \(f(x)\) definida em quatro pontos distintos \(x_0\), \(x_1\), \(x_2\) e \(x_3\) equidistantes no intervalo \([a,b]\). O polinômio interpolador de Lagrange para esses pontos, considerando a mudança de variável \(u = \frac{x-x_0}{h}\) é dado por

\[P_3(u)=f(x_0) \left[ \frac{(u-1)(u-2)(u-3)}{-6}\right] + f(x_1) \left[ \frac{u(u-2)(u-3)}{2} \right] + f(x_2) \left[ \frac{u(u-1)(u-3)}{-2}\right]+ f(x_3)\left[ \frac{u(u-1)(u-2)}{6} \right]\]

ou

\[P_3(u)=f(x_0) \left[ \frac{u^3-6u^2+11u-6}{-6}\right] + f(x_1) \left[ \frac{u^3-5u^2+6u}{2} \right] + f(x_2) \left[ \frac{u^3-4u^2+3u}{-2}\right] + f(x_3)\left[ \frac{u^3-5u^2+6u}{6} \right]\]

O que fornece

\[ \int_{x_0}^{x_3} f(x) dx \approx h \int_{0}^{3} P_3(u) du = \frac{3}{8}h \left[f(x_0)+3f(x_1)+3f(f_2)+f(x_3) \right]\]

Então

\[\int_{x_0}^{x_3} f(x) dx \approx \frac{3}{8}h \left[f(x_0)+3f(x_1)+3f(x_2)+f(x_3) \right]\]

que consiste na regra 3/8 de Simpson.

Graficamente, tem-se

Figura 6.5 - Aproximação pela integral do polinômio interpolador de grau 3

Um limitante superior para o erro será dado por

\[ |E_3| \leq \frac{3h^5}{80} max.\{|f^{(4)}(x)|, x_0 \leq \xi \leq x_3 \}\]

Exemplo 6.5: Calcule o valor aproximado da integral \(\int_1^7 ln(x+9) dx\) usando a regra 3/8 de Simpson.

x = np.linspace(1,7,4)
h = x[1]-x[0]
f = lambda x: np.log(x+9)
I = (3*h/8)*(f(x[0]) + 3*f(x[1])+3*f(x[2])+f(x[3]))
print(I)

15.335299315082702

print(integrate.simpson(f(x), x=np.linspace(1,7,4)))

15.335928614229697

A regra 3/8 de Simpson repetida (ou generalizada) consiste em subdividir o intervalo de integração \([a,b]\) em \(n\) subintervalos de ampliture \(h\), em que \(n\) é um número múltiplo de 3, com \(x_0=a\) e \(x_n=b\), então, aplicar a regra 3/8 de Simpson repetidamente a cada 3 subintervalos consecutivos. Com isso obtém-se:

\[ \int_{x_0}^{x_n} f(x) dx \approx \frac{3}{8}h \left[ f(x_0) + 3f(x_1)+3f(x_2)+f(x_3) \right] + \frac{3}{8}h \left[f(x_3)+3f(x_4)+3f(x_5)+f(x_6) \right] + ... + \frac{3}{8}h \left[f(x_{n-3})+3f(x_{n-2})+3f(x_{n-1})+f(x_n) \right]\]

\[ = \frac{3}{8}h \left\{ f(x_0) + 3 \left[f(x_1)+f(x_2)+f(x_4)+f(x_5)+....+ f(x_{n-2})+f(x_{n-1})\right] + 2 \left[f(x_3)+f(x_6)+....+f(x_{n-3}) \right] + f(x_n)\right\}\]

que consiste na regra 3/8 de Simpson repetida.

Um limitante superior para o erro é dado por

\[ |E_3| \leq \frac{h^4}{80}(x_n-x_0) \,\, max.\left\{\left|f^{(4)}(x)\right|, x_0 \leq \xi \leq x_n \right\}\]

Exemplo 2: Calcule o valor aproximado da integral \(\int_1^6 ln(x+9) dx\) usando a regra 3/8 de Simpson para 8, 20 e 40 subintervalos.

x0 = 1.0; xn = 6.0 
f = lambda x: np.log(x+9)

for n in [4,20,40]:
    h = (xn-x0)/n
    x = np.linspace(x0, xn, n+1) 
    y = f(x)
    # Regra 3/8 de Simpson usando funções do numpy
    I = (3*h/8)*(y[0] + 3*np.sum(y[1:n-1:3]+y[2:n:3]) +\
                 2*np.sum(y[3:n:3])+ y[-1])
    print ("n=",n,", I=",I)

n= 4 , I= 11.761407778686316
n= 20 , I= 11.75388556350441
n= 40 , I= 12.510405538009266

O sub-pacote scipy.integrate, de SciPy, provê diversas funções para integração numérica, incluindo as regras de Newton-Cotes trapezoid, cumulative_trapezoid e simpson. Além destas, outras funções disponíveis são quad, dblquad e tplquad para integrais simples, duplas e triplas, respectivamente; fixed_quad e quadraturepara quadratura Gaussiana e; rombergpara integração de Romberg.

Exercícios:

Encontre, se possível, a primitiva das seguintes funções, então obtenha a solução exata e compare com soluções numéricas usando somas de Riemann e os métodos de Newton-Cotes para diferentes números de subintervalos. Compare os resultados.

a) \(\int_{1}^{1.6} \frac{2x}{x^2-4} dx\)

b) \(\int_{0}^{1} x^2 e^{-x} dx\)

c) \(\int_{0}^{\pi/4} e^{x^3}sen(2x)dx\)

d) \(\int_{0}^{0.5} \frac{2}{x-4} dx\)

e) \(\int_{0}^{1} x^{-1/4}sen(x) dx\)

f) \(\int_{0}^{1} \frac{e^{2x}}{\sqrt[5]{x^2}}dx\)

g) \(\int_{0}^{1} \frac{ln(x)}{(1-x)^{1/5}}dx\)

h) \(\int_{0}^{1} \frac{cos(2x)}{x^{1/3}}dx\)

i) \(\int e^{x^2} dx\)

j) \(\int \frac{e^x}{x} dx\)

k) \(\int sen(x^2) dx\)

l) \(\int ln(lnx) dx\)

m) \(\int e^{-\frac{x^2}{2}} dx\)

n) \(\int cos(x^2) dx\)

o) \(\int cos(e^x) dx\)

p) \(\int \frac{1}{ln(x)} dx\)